Negative Binomial Distribution Calculator

1. What is the Negative Binomial Distribution Calculator?

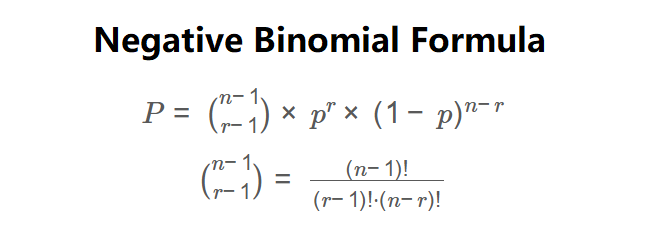
Definition: The Negative Binomial Distribution Calculator computes the probability of achieving a fixed number of successes in a specific number of trials, along with the number of combinations, for a negative binomial distribution.

Purpose: This tool helps analyze scenarios involving repeated trials until a specified number of successes, such as in quality control, marketing campaigns, or games.

2. How Does the Calculator Work?

The calculator uses the following formulas:

\( P = \binom{n-1}{r-1} \times p^r \times (1-p)^{n-r} \)

\( \binom{n-1}{r-1} = \frac{(n-1)!}{(r-1)! \cdot (n-r)!} \)

Where:

\( n \): Number of trials;
\( r \): Number of successes;
\( p \): Probability of success;
\( P \): Probability of r-th success on n-th trial;
\( \binom{n-1}{r-1} \): Binomial coefficient (combinations).

Steps:

Enter the number of trials (n), number of successes (r), and probability of success (p).
Calculate the binomial coefficient: (n-1)! divided by (r-1)! times (n-r)!.
Calculate the probability: binomial coefficient times p to the power r times (1-p) to the power (n-r).
Display probability as a percentage and combinations, using scientific notation for values less than 0.0001.

3. Importance of the Negative Binomial Distribution Calculation

Calculating negative binomial probabilities is essential for:

Statistical Analysis: Models the number of trials needed for a fixed number of successes in experiments.
Decision Making: Helps estimate outcomes in scenarios like marketing or quality control where successes are counted.
Risk Assessment: Evaluates the likelihood of achieving goals within a certain number of attempts.

4. Using the Calculator

Example: Calculate the probability of needing 5 trials to achieve 2 successes when flipping a fair coin (p = 0.5):

Input: Number of Trials: 5; Number of Successes: 2; Probability of Success: 0.5.
Combinations: \( \binom{5-1}{2-1} = \binom{4}{1} = \frac{4!}{1! \cdot 3!} = 4 \).
Probability: \( 4 \times 0.5^2 \times (1-0.5)^{5-2} = 4 \times 0.25 \times 0.125 = 0.125 \).
Result: Probability P(Y=5): 12.5000%; Combinations (4,1): 4.0000.

5. Frequently Asked Questions (FAQ)

Q: What is the negative binomial distribution?
A: It models the number of trials needed to achieve a fixed number of successes in independent Bernoulli trials with constant success probability.

Q: How does it differ from the binomial distribution?
A: The binomial distribution models the number of successes in a fixed number of trials, while the negative binomial models the number of trials until a fixed number of successes.

Q: What are practical applications of this calculator?
A: It’s used in quality control, marketing, and games to estimate the number of attempts needed for a target number of successes.