Error Propagation Calculator

Mathematical Operation:

X Value:

Uncertainty in X (ΔX):

Y Value:

Uncertainty in Y (ΔY):

1. What is the Error Propagation Calculator?

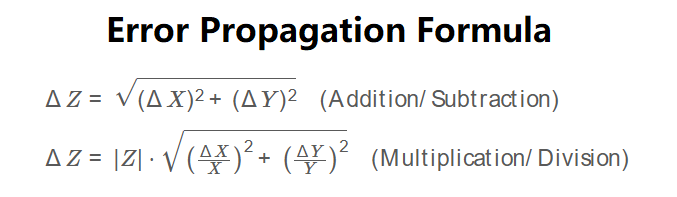
Definition: The Error Propagation Calculator computes the result and uncertainty of a mathematical operation (addition, subtraction, multiplication, or division) involving two variables with known uncertainties.

Purpose: This tool is used in physics, engineering, and statistics to evaluate how uncertainties in measurements affect the final result, ensuring accurate error estimation in calculations.

2. How Does the Calculator Work?

The calculator uses the following formulas:

\( \Delta Z = \sqrt{(\Delta X)^2 + (\Delta Y)^2} \quad \text{(Addition/Subtraction)} \)

\( \Delta Z = |Z| \cdot \sqrt{\left(\frac{\Delta X}{X}\right)^2 + \left(\frac{\Delta Y}{Y}\right)^2} \quad \text{(Multiplication/Division)} \)

Where:

\( X, Y \): Measured values;
\( \Delta X, \Delta Y \): Uncertainties in X and Y;
\( Z \): Result of the operation;
\( \Delta Z \): Uncertainty in the result.

Steps:

Select the mathematical operation (Addition, Subtraction, Multiplication, or Division).
Enter values for X, Y, and their uncertainties (ΔX, ΔY).
Compute Z based on the operation (e.g., \( Z = X + Y \)).
Calculate ΔZ using the appropriate error propagation formula.
Display results formatted to four decimal places or scientific notation.

3. Importance of Error Propagation

Error propagation is essential for:

Measurement Accuracy: Ensures reliable results in experiments by accounting for measurement uncertainties.
Scientific Analysis: Critical in physics, engineering, and data science for precise calculations.
Error Management: Helps quantify how errors in inputs affect derived quantities.

4. Using the Calculator

Example: Calculate the error propagation for adding two rod lengths: \( X = 2.00 \pm 0.03 \) m, \( Y = 0.88 \pm 0.04 \) m.

Input: Operation: Addition, X: 2.00, ΔX: 0.03, Y: 0.88, ΔY: 0.04
Result: \( Z = 2.00 + 0.88 = 2.88 \) m
Uncertainty: \( \Delta Z = \sqrt{(0.03)^2 + (0.04)^2} \approx 0.05 \) m
Result: Z: 2.8800, ΔZ: 0.0500

5. Frequently Asked Questions (FAQ)

Q: What is error propagation?
A: Error propagation quantifies how uncertainties in measured values affect the uncertainty in a calculated result.

Q: Why are different formulas used for addition/subtraction vs. multiplication/division?
A: Addition/subtraction errors combine in quadrature, while multiplication/division errors use relative uncertainties due to the nature of the operations.

Q: Why can’t Y be zero in division?
A: Division by zero is undefined, and error propagation for division requires non-zero denominators.