db Gain Calculator

db Gain Calculator - Calculate Power gain, Voltage Gain, Current Gain, Microvolts and Microamps Conversion

Calculate:

1. What is the Decibel Conversion Calculator?

Definition: This calculator computes decibel values for various quantities (power, voltage, current, milliwatts, microvolts, microamps) using logarithmic formulas to express ratios or levels relative to a reference value.

Purpose: It is used in electronics, audio engineering, telecommunications, and signal processing to quantify signal strength, compare power or voltage levels, and analyze system performance.

2. How Does the Calculator Work?

The calculator uses the following decibel conversion formulas:

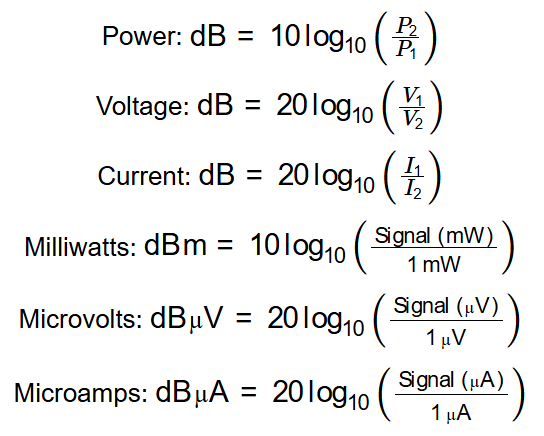
Power: \( \text{dB} = 10 \log_{10} \left( \frac{P_2}{P_1} \right) \)
Voltage: \( \text{dB} = 20 \log_{10} \left( \frac{V_1}{V_2} \right) \)
Current: \( \text{dB} = 20 \log_{10} \left( \frac{I_1}{I_2} \right) \)
Milliwatts: \( \text{dBm} = 10 \log_{10} \left( \frac{\text{Signal (mW)}}{1 \, \text{mW}} \right) \)
Microvolts: \( \text{dBµV} = 20 \log_{10} \left( \frac{\text{Signal (µV)}}{1 \, \text{µV}} \right) \)
Microamps: \( \text{dBµA} = 20 \log_{10} \left( \frac{\text{Signal (µA)}}{1 \, \text{µA}} \right) \)

Steps:

Select the type of decibel conversion (Power, Voltage, Current, Milliwatts, Microvolts, or Microamps).
Enter the required input values (e.g., \( P_2 \) and \( P_1 \) for power, or signal value for dBm, dBµV, dBµA).
Validate inputs to ensure they are non-negative and denominators are non-zero.
Calculate the decibel value using the appropriate formula.
Format the result in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.
Display the result with the appropriate unit (dB, dBm, dBµV, or dBµA).

3. Importance of Decibel Conversion

Calculating decibel values is crucial for:

Signal Analysis: Comparing signal strengths in communication systems, audio equipment, and RF engineering.
System Design: Ensuring proper gain or attenuation in amplifiers, filters, and other electronic components.
Measurement Standards: Using standardized units like dBm, dBµV, and dBµA for consistent reporting in telecommunications and electronics.

4. Using the Calculator

Example 1 (Calculating Power dB): Calculate the decibel difference for two power levels:

Calculate: Power (dB);
Power \( P_2 \): 10 W;
Power \( P_1 \): 1 W;
Decibel: \( \text{dB} = 10 \log_{10} \left( \frac{10}{1} \right) = 10 \log_{10} (10) = 10 \times 1 = 10.0000 \, \text{dB} \).

Example 2 (Calculating dBm): Calculate the power in dBm for a signal:

Calculate: Milliwatts (dBm);
Signal Power: 1 mW;
dBm: \( \text{dBm} = 10 \log_{10} \left( \frac{1}{1} \right) = 10 \log_{10} (1) = 0.0000 \, \text{dBm} \).

Example 3 (Calculating dBµV): Calculate the voltage in dBµV:

Calculate: Microvolts (dBµV);
Signal Voltage: 100 µV;
dBµV: \( \text{dBµV} = 20 \log_{10} \left( \frac{100}{1} \right) = 20 \log_{10} (100) = 20 \times 2 = 40.0000 \, \text{dBµV} \).

5. Frequently Asked Questions (FAQ)

Q: What is a decibel?
A: A decibel (dB) is a logarithmic unit used to express the ratio of two values, such as power, voltage, or current, commonly used in electronics and audio engineering.

Q: Why use dBm, dBµV, or dBµA?
A: These units measure power, voltage, or current relative to a fixed reference (1 mW, 1 µV, 1 µA), providing a standardized way to express signal levels in telecommunications and RF systems.

Q: Why do voltage and current use 20 instead of 10 in the formula?
A: Voltage and current dB calculations use 20 because power is proportional to the square of voltage or current (\( P = V^2/R \) or \( P = I^2 R \)), and the logarithmic transformation results in a factor of 20 when expressing voltage or current ratios in dB.