Planetary Temperature Calculator

Calculate:

Albedo (α): (0 to 1)

Distance (d):

Solar Constant (S₀): W/m²

Temperature (T):

1. What is a Planetary Temperature Calculator?

Definition: This calculator determines the effective temperature, albedo, distance, or solar constant of a planet based on the provided inputs, assuming it behaves as a blackbody.

Purpose: It is used in astronomy to estimate planetary properties, aiding in habitability assessments, climate modeling, and exoplanet studies.

2. How Does the Calculator Work?

The calculator uses the energy balance equation:

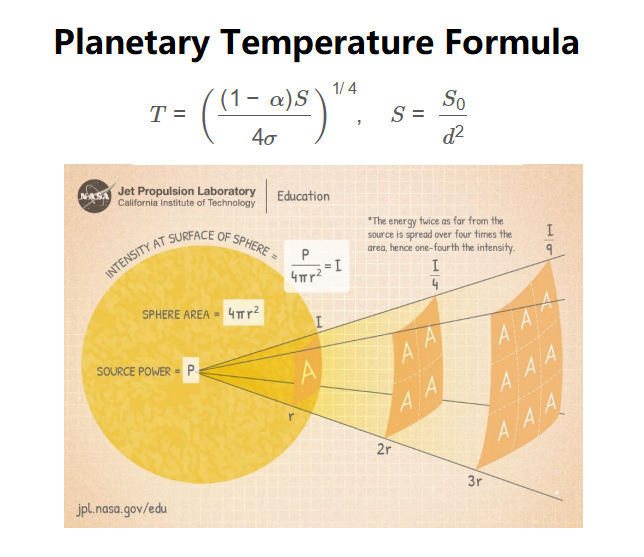
\[ T = \left( \frac{(1 - \alpha) S}{4 \sigma} \right)^{1/4}, \quad S = \frac{S_0}{d^2} \] Where:

\( T \): Effective temperature (K, °C, °F)
\( \alpha \): Albedo (0 to 1)
\( S \): Solar constant at distance \( d \) (W/m²)
\( S_0 \): Solar constant at 1 AU (W/m²)
\( d \): Distance (AU, km, miles)
\( \sigma \): Stefan-Boltzmann constant, \( 5.67 \times 10^{-8} \, \text{W/m}^2\text{K}^4 \)

Calculations:

Temperature (T): \( T = \left( \frac{(1 - \alpha) S_0 / d^2}{4 \sigma} \right)^{1/4} \)
Albedo (α): \( \alpha = 1 - \frac{4 \sigma T^4}{S_0 / d^2} \)
Distance (d): \( d = \sqrt{\frac{S_0}{(4 \sigma T^4) / (1 - \alpha)}} \)
Solar Constant (S₀): \( S_0 = \frac{4 \sigma T^4}{1 - \alpha} \cdot d^2 \)

Unit Conversions:

Distance (d): AU, km (1 AU = 1.496 × 10⁸ km), miles (1 AU = 9.296 × 10⁷ miles)
Temperature (T): K, °C (K = °C + 273.15), °F (°F = (°C × 9/5) + 32)
Solar Constant (S₀): W/m²

Steps:

Select what to calculate: Temperature, Albedo, Distance, or Solar Constant.
Enter known values with appropriate units.
Convert inputs to base units (AU, K, W/m²).
Perform the calculation using the appropriate formula.
Convert the result to the selected unit and display.

3. Importance of Planetary Temperature Calculation

Calculating these parameters is crucial for:

Habitability: Assessing if a planet’s temperature supports liquid water.
Climate Modeling: Understanding atmospheric effects like the greenhouse effect.
Exoplanet Studies: Analyzing distant planets’ properties.
Education: Teaching energy balance and astrophysics concepts.

4. Using the Calculator

Examples:

Example 1 (Temperature): For \( \alpha = 0.3 \), \( d = 1 \, \text{AU} \), \( S_0 = 1366 \, \text{W/m}^2 \):
- \( S = 1366 / 1^2 = 1366 \, \text{W/m}^2 \)
- \( T = \left( \frac{(1 - 0.3) \times 1366}{4 \times 5.67 \times 10^{-8}} \right)^{1/4} \approx 255 \, \text{K} \)
- In °C: \( 255 - 273.15 = -18.150 \, \text{°C} \)
Example 2 (Albedo): For \( T = 255 \, \text{K} \), \( d = 1 \, \text{AU} \), \( S_0 = 1366 \, \text{W/m}^2 \):
- \( S = 1366 / 1^2 = 1366 \, \text{W/m}^2 \)
- \( \alpha = 1 - \frac{4 \times 5.67 \times 10^{-8} \times 255^4}{1366} \approx 0.300 \)
Example 3 (Distance): For \( T = 255 \, \text{K} \), \( \alpha = 0.3 \), \( S_0 = 1366 \, \text{W/m}^2 \):
- \( d = \sqrt{\frac{1366}{(4 \times 5.67 \times 10^{-8} \times 255^4) / (1 - 0.3)}} \approx 1 \, \text{AU} \)
- In km: \( 1 \times 1.496 \times 10^8 = 1.496 \times 10^8 \, \text{km} \)
Example 4 (Solar Constant): For \( T = 255 \, \text{K} \), \( \alpha = 0.3 \), \( d = 1 \, \text{AU} \):
- \( S_0 = \frac{4 \times 5.67 \times 10^{-8} \times 255^4}{1 - 0.3} \times 1^2 \approx 1366 \, \text{W/m}^2 \)

5. Frequently Asked Questions (FAQ)

Q: What is effective temperature?
A: It’s the temperature a planet would have as a blackbody, balancing absorbed and radiated energy, excluding atmospheric effects.

Q: Why is albedo important?
A: Albedo determines how much sunlight is reflected; higher albedo lowers temperature.

Q: How does distance affect temperature?
A: Temperature scales as \( T \propto d^{-1/2} \), so farther planets are colder.

Q: What is the solar constant?
A: It’s the solar energy flux at 1 AU, typically 1366 W/m² for the Sun.