e Power X Calculator

1. What is an e Power X Calculator?

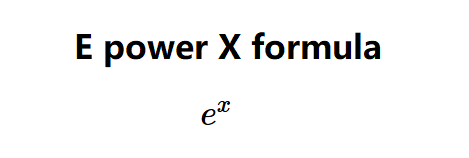
Definition: This calculator computes the value of \( e^x \), where \( e \) is the base of the natural logarithm (approximately 2.71828) and \( x \) is the exponent provided by the user. The function \( e^x \) is also known as the exponential function with base \( e \).

Purpose: It aids in mathematics, science, and engineering by calculating exponential growth or decay, commonly used in calculus, physics, and financial modeling.

2. How Does the Calculator Work?

The calculator uses the following formula:

Exponential: \( e^x \)

Steps:

Input the exponent \( x \) (any real number).
Compute \( e^x \) using the exponential function.
Format the output to 4 decimal places or scientific notation for very small or large values.

3. Importance of e Power X Calculations

Calculating \( e^x \) is essential for:

Mathematics Education: Understanding the exponential function and its role in calculus.
Science and Engineering: Modeling natural phenomena like radioactive decay, population growth, or heat dissipation.
Finance: Calculating continuous compound interest or growth rates.

4. Using the Calculator

Examples:

Example 1: Exponent \( x = 1 \)
Result: \( e^1 \approx 2.7183 \).
Example 2: Exponent \( x = 0 \)
Result: \( e^0 = 1.0000 \).
Example 3: Exponent \( x = -2 \)
Result: \( e^{-2} \approx 0.1353 \).

5. Frequently Asked Questions (FAQ)

Q: What is \( e \)?
A: \( e \) is the base of the natural logarithm, an irrational number approximately equal to 2.71828, fundamental in mathematics and science.

Q: Why is \( e^x \) important?
A: The function \( e^x \) is the natural exponential function, widely used in modeling continuous growth or decay, and it’s the eigenfunction of differentiation (\( \frac{d}{dx} e^x = e^x \)).

Q: Can the exponent \( x \) be negative?
A: Yes, \( x \) can be any real number. A negative \( x \) results in a value between 0 and 1, as \( e^x \) is always positive.