Truncated Cone Volume Calculator

Top Radius (\( r \)):

Base Radius (\( R \)):

Height (\( h \)):

Slant Height (\( s \)):

Volume:

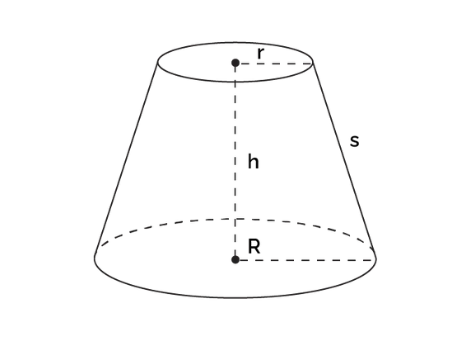
1. What is a Truncated Cone Volume Calculator?

Definition: This calculator computes the slant height (\( s \)) and volume of a truncated cone (frustum of a cone), given the top radius (\( r \)), base radius (\( R \)), and height (\( h \)). A truncated cone is a cone with its top portion removed, resulting in two parallel circular bases of different radii connected by a curved surface.

Purpose: It aids in geometry education, engineering, and design by calculating key parameters for applications like manufacturing (e.g., conical containers, funnels), architecture (e.g., truncated conical structures), and material estimation.

2. How Does the Calculator Work?

The calculator takes the top radius (\( r \)), base radius (\( R \)), and height (\( h \)) with independently selected units (m, cm, mm, in, ft, yd) and computes:

Slant Height (\( s \)):
- Formula: \( s = \sqrt{(R - r)^2 + h^2} \).
- The distance from a point on the edge of the base to a point on the edge of the top, forming a right triangle with the height and radius difference.
Volume:
- Formula: \( V = \frac{1}{3} \pi h (R^2 + r^2 + R r) \).
- The space occupied by the frustum, calculated as one-third the height times the sum of the base areas and their geometric mean.

Unit Conversions:

Length Units: m, cm (1 m = 100 cm), mm (1 m = 1000 mm), in (1 m = 39.3701 in), ft (1 m = 3.28084 ft), yd (1 m = 1.09361 yd).
Volume Units: m³, cm³ (1 m³ = 1000000 cm³), mm³ (1 m³ = 1000000000 mm³), in³ (1 m³ = 61023.7441 in³), ft³ (1 m³ = 35.3147 ft³), yd³ (1 m³ = 1.30795 yd³).

Steps:

Input the top radius (\( r \)), base radius (\( R \)), and height (\( h \)) with their respective units.
Validate inputs (\( r \geq 0 \), \( R \geq 0 \), \( h > 0 \)).
Convert inputs to meters for calculations.
Compute slant height and volume.
Convert each result to its independently selected output unit and format to 4 decimal places or scientific notation for small values.

3. Importance of Truncated Cone Volume Calculations

Calculating truncated cone parameters is crucial for:

Geometry Education: Understanding the properties of conical frustums and their volume calculations.
Engineering and Manufacturing: Designing objects like buckets, lampshades, or funnels, and estimating material or liquid capacity.
Architecture: Creating structures with frustum-shaped elements, such as decorative columns or roof sections.

4. Using the Calculator

Examples:

Example 1: Top Radius \( r = 3 \, \text{cm} \), Base Radius \( R = 5 \, \text{cm} \), Height \( h = 4 \, \text{cm} \), Output units: cm, cm³
Convert: \( r = 0.03 \, \text{m} \), \( R = 0.05 \, \text{m} \), \( h = 0.04 \, \text{m} \).
Slant Height: \( s = \sqrt{(0.05 - 0.03)^2 + 0.04^2} \approx 0.0447 \, \text{m} = 4.4721 \, \text{cm} \).
Volume: \( V = \frac{1}{3} \pi \times 0.04 \times (0.05^2 + 0.03^2 + 0.05 \times 0.03) \approx 0.0001885 \, \text{m}^3 = 188.4956 \, \text{cm}^3 \).
Example 2: Top Radius \( r = 1 \, \text{m} \), Base Radius \( R = 2 \, \text{m} \), Height \( h = 3 \, \text{m} \), Output units: ft, m³
Slant Height: \( s = \sqrt{(2 - 1)^2 + 3^2} \approx 3.1623 \, \text{m} = 10.3747 \, \text{ft} \).
Volume: \( V = \frac{1}{3} \pi \times 3 \times (2^2 + 1^2 + 2 \times 1) \approx 21.9911 \, \text{m}^3 \).
Example 3: Top Radius \( r = 4 \, \text{in} \), Base Radius \( R = 6 \, \text{cm} \), Height \( h = 5 \, \text{in} \), Output units: in, in³
Convert: \( r = 0.1016 \, \text{m} \), \( R = 0.06 \, \text{m} \), \( h = 0.1270 \, \text{m} \).
Slant Height: \( s = \sqrt{(0.06 - 0.1016)^2 + 0.1270^2} \approx 0.1333 \, \text{m} = 5.2507 \, \text{in} \).
Volume: \( V \approx 0.0007536 \, \text{m}^3 = 46.0085 \, \text{in}^3 \).

5. Frequently Asked Questions (FAQ)

Q: What is a truncated cone?
A: A truncated cone, or frustum, is a cone with its top portion removed, resulting in two parallel circular bases of different radii connected by a curved surface.

Q: Why is the slant height important?
A: The slant height is the distance along the curved surface from the edge of the base to the edge of the top, used in calculations for lateral surface area and structural design.

Q: Can I use different units for inputs and outputs?
A: Yes, the calculator allows independent unit selection for top radius, base radius, height, slant height, and volume, enabling flexible conversions (e.g., radius in centimeters, volume in cubic inches).