Trapezoidal Prism Volume Calculator

Height \( h \):

Length \( L \):

Long base \( B \):

Short base \( b \):

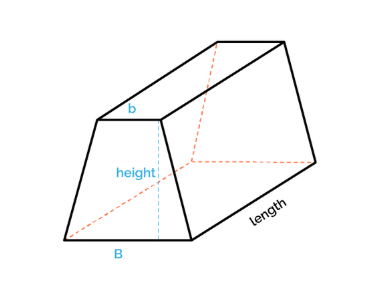
1. What is a Trapezoidal Prism Volume Calculator?

Definition: This calculator computes the volume (\( V \)) of a trapezoidal prism, given the height (\( h \)) of the trapezoidal base, the length (\( L \)) of the prism, and the lengths of the long base (\( B \)) and short base (\( b \)) of the trapezoidal base. A trapezoidal prism is a three-dimensional shape with two parallel trapezoidal bases connected by four rectangular or parallelogram faces.

Purpose: It aids in geometry education, engineering, and design by calculating the volume for trapezoidal prism structures, such as in architecture, packaging, or material estimation.

2. How Does the Calculator Work?

The calculator uses the following formula for a trapezoidal prism:

Volume: \( V = \frac{1}{2} (B + b) h L \).

Unit Conversions:

Length Units: m, cm (1 m = 100 cm), mm (1 m = 1000 mm), in (1 m = 39.3701 in), ft (1 m = 3.28084 ft), yd (1 m = 1.09361 yd).
Volume Units: m³, cm³ (1 m³ = 1000000 cm³), mm³ (1 m³ = 1000000000 mm³), in³ (1 m³ = 61023.7441 in³), ft³ (1 m³ = 35.3147 ft³), yd³ (1 m³ = 1.30795 yd³).

Steps:

Input the height \( h \), length \( L \), long base \( B \), and short base \( b \), and select their units.
Validate inputs (must be positive, and \( B > b \)).
Convert inputs to meters for calculations.
Compute the volume using the formula above.
Convert the output to the selected volume unit.
Format the output to 4 decimal places or scientific notation for small values.

3. Importance of Trapezoidal Prism Volume Calculations

Calculating the volume of a trapezoidal prism is essential for:

Geometry Education: Understanding three-dimensional shapes and their properties.
Architecture and Engineering: Designing structures with trapezoidal cross-sections, such as ramps, roofs, or channels.
Manufacturing and Packaging: Determining material requirements or storage capacity for trapezoidal prism-shaped objects.

4. Using the Calculator

Examples:

Example 1: Height \( h = 4 \, \text{cm} \), Length \( L = 10 \, \text{cm} \), Long base \( B = 8 \, \text{cm} \), Short base \( b = 6 \, \text{cm} \)
Convert: \( h = 0.04 \, \text{m} \), \( L = 0.1 \, \text{m} \), \( B = 0.08 \, \text{m} \), \( b = 0.06 \, \text{m} \).
Volume: \( V = \frac{1}{2} \times (0.08 + 0.06) \times 0.04 \times 0.1 \approx 0.00028 \, \text{m}^3 = 280.0000 \, \text{cm}^3 \).
Example 2: Height \( h = 2 \, \text{m} \), Length \( L = 5 \, \text{m} \), Long base \( B = 4 \, \text{m} \), Short base \( b = 3 \, \text{m} \)
Volume: \( V = \frac{1}{2} \times (4 + 3) \times 2 \times 5 \approx 35.0000 \, \text{m}^3 \).

5. Frequently Asked Questions (FAQ)

Q: What is a trapezoidal prism?
A: A trapezoidal prism is a three-dimensional shape with two parallel trapezoidal bases (one with parallel sides B and b) connected by four faces, typically rectangles or parallelograms.

Q: Why must the long base be greater than the short base?
A: The long base (\( B \)) must be greater than the short base (\( b \)) to define a valid trapezoid, where the parallel sides have different lengths.

Q: How is the volume formula derived?
A: The volume is the area of the trapezoidal base (\( \frac{1}{2} (B + b) h \)) multiplied by the prism’s length (\( L \)), as the prism extends uniformly along its length.