1. What is a Supplementary Angles Calculator?

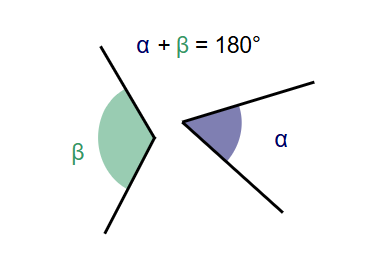
Definition: This calculator computes the supplementary angle for a given angle. Supplementary angles are two angles whose measures sum to 180° (or π radians), forming a straight line when adjacent.

Purpose: It simplifies geometric calculations by finding the angle that complements a given angle to reach 180°, useful in geometry, trigonometry, and design.

2. How Does the Calculator Work?

The calculator uses the following formulas:

• Supplementary Angle (degrees): \( \theta_{\text{supp}} = 180^\circ - \theta \).
• Supplementary Angle (radians): \( \theta_{\text{supp}} = \pi - \theta \).
• Unit Conversion:
  • Degrees to radians: \( \text{radians} = \text{degrees} \times \frac{\pi}{180} \).
  • Radians to degrees: \( \text{degrees} = \text{radians} \times \frac{180}{\pi} \).

Steps:

• Input the angle \( \theta \) and select its unit (degrees or radians).
• Validate the input (must be 0° to 180° or 0 to π radians).
• Convert the angle to degrees for processing.
• Calculate the supplementary angle by subtracting from 180°.
• Convert the supplementary angle to the selected output unit (degrees or radians).
• Format the output to 4 decimal places or scientific notation for small values.

3. Importance of Supplementary Angle Calculations

Calculating supplementary angles is crucial for:

• Geometry: Understanding relationships in shapes like parallelograms, trapezoids, and linear pairs where angles sum to 180°.
• Trigonometry: Simplifying calculations, as trigonometric functions of supplementary angles are related (e.g., \( \sin(\theta) = \sin(180^\circ - \theta) \)).
• Design and Engineering: Ensuring angles in structures or designs form straight lines, such as in architecture or machinery.

4. Using the Calculator

Examples:

• Example 1: Angle \( \theta = 70^\circ \)
  • Supplementary Angle: \( \theta_{\text{supp}} = 180^\circ - 70^\circ = 110^\circ \).
  • In radians: \( 110 \times \frac{\pi}{180} \approx 1.9199 \, \text{rad} \).
• Example 2: Angle \( \theta = \frac{\pi}{4} \, \text{rad} \)
  • Convert: \( \frac{\pi}{4} \times \frac{180}{\pi} = 45^\circ \).
  • Supplementary Angle: \( 180^\circ - 45^\circ = 135^\circ \).
  • In radians: \( 135 \times \frac{\pi}{180} = \frac{3\pi}{4} \approx 2.3562 \, \text{rad} \).

5. Frequently Asked Questions (FAQ)

Q: What are supplementary angles?
A: Supplementary angles are two angles whose measures sum to 180° (or π radians). They form a straight line if adjacent but can also be non-adjacent.

Q: Can supplementary angles be greater than 180°?
A: No, each angle must be 0° to 180° (or 0 to π radians) to have a positive supplementary angle, as their sum must exactly equal 180°.

Supplementary Angles Calculator© - All Rights Reserved 2025