Square in a Circle Calculator

Mode:

Radius of the Circle \( r \):

Area of the Circle \( A \):

Side of Square \( s \):

Area of Square \( A_s \):

1. What is a Square in a Circle Calculator?

Definition: This calculator computes geometric relationships between a square and a circle, including the largest square inside a circle, the largest circle inside a square, a square with the same area as a circle, and a circle with the same area as a square.

Purpose: It assists in solving problems involving squares and circles, useful in geometry education, engineering, and design.

2. How Does the Calculator Work?

The calculator operates in four modes:

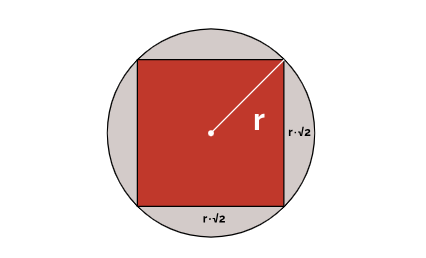
Largest Square in a Circle:

Area of the Circle \( A \): \( A = \pi \times r^2 \)
Side of Square \( s \): \( s = r \times \sqrt{2} \) (diagonal of square = diameter of circle)
Area of Square \( A_s \): \( A_s = s^2 \)

Largest Circle in a Square:

Area of the Square \( A \): \( A = s^2 \)
Radius of Circle \( r \): \( r = \frac{s}{2} \) (diameter of circle = side of square)
Area of Circle \( A_c \): \( A_c = \pi \times r^2 \)

Square with Same Area as Circle:

Area of the Circle \( A \): \( A = \pi \times r^2 \)
Area of the Square \( A \): \( A = \pi \times r^2 \)
Side of the Square \( s \): \( s = \sqrt{A} \)

Circle with Same Area as Square:

Area of the Square \( A \): \( A = s^2 \)
Area of the Circle \( A \): \( A = s^2 \)
Radius of the Circle \( r \): \( r = \sqrt{\frac{A}{\pi}} \)

Unit Conversions:

Input Dimensions: m, cm (1 m = 100 cm), mm (1 m = 1000 mm), in (1 m = 39.3701 in), ft (1 m = 3.28084 ft), yd (1 m = 1.09361 yd)
Output Dimensions: m, cm, mm, in, ft, yd
Output Area: m², cm² (1 m² = 10000 cm²), mm² (1 m² = 1000000 mm²), in² (1 m² = 1550.0031 in²), ft² (1 m² = 10.7639 ft²), yd² (1 m² = 1.19599 yd²)

Steps:

Select the mode (Largest Square in a Circle, Largest Circle in a Square, Square with Same Area as Circle, or Circle with Same Area as Square).
View the corresponding diagram for the selected mode.
Input the required value (radius \( r \) or side \( s \)) with its unit.
Convert the input to meters for calculation.
Validate the input (must be positive).
Calculate the outputs based on the mode's formulas, formatted to 4 decimal places or in scientific notation for very small values.

3. Importance of Square in a Circle Calculations

Calculating relationships between squares and circles is crucial for:

Geometry Education: Understanding the geometric properties and relationships between shapes.
Engineering Design: Designing components where squares and circles must fit together, such as in packaging or machinery.
Construction: Optimizing space and material usage in circular or square layouts.

4. Using the Calculator

Examples:

Largest Square in a Circle: For \( r = 2 \, \text{cm} \):
- Convert: \( r = 0.02 \, \text{m} \)
- Area of the Circle: \( A = \pi \times (0.02)^2 \approx 0.001257 \, \text{m}^2 \)
- Side of Square: \( s = 0.02 \times \sqrt{2} \approx 0.0283 \, \text{m} \)
- Area of Square: \( A_s = (0.0283)^2 \approx 0.0008 \, \text{m}^2 \)
- Convert: \( A \approx 12.57 \, \text{cm}^2 \), \( s \approx 2.83 \, \text{cm} \), \( A_s \approx 8 \, \text{cm}^2 \)
Largest Circle in a Square: For \( s = 4 \, \text{cm} \):
- Convert: \( s = 0.04 \, \text{m} \)
- Area of the Square: \( A = (0.04)^2 = 0.0016 \, \text{m}^2 \)
- Radius of Circle: \( r = \frac{0.04}{2} = 0.02 \, \text{m} \)
- Area of Circle: \( A_c = \pi \times (0.02)^2 \approx 0.001257 \, \text{m}^2 \)
- Convert: \( A = 16 \, \text{cm}^2 \), \( r = 2 \, \text{cm} \), \( A_c \approx 12.57 \, \text{cm}^2 \)
Square with Same Area as Circle: For \( r = 3 \, \text{cm} \):
- Convert: \( r = 0.03 \, \text{m} \)
- Area of the Circle: \( A = \pi \times (0.03)^2 \approx 0.002827 \, \text{m}^2 \)
- Area of the Square: \( A = 0.002827 \, \text{m}^2 \)
- Side of the Square: \( s = \sqrt{0.002827} \approx 0.0532 \, \text{m} \)
- Convert: \( A \approx 28.27 \, \text{cm}^2 \), \( s \approx 5.32 \, \text{cm} \)
Circle with Same Area as Square: For \( s = 5 \, \text{cm} \):
- Convert: \( s = 0.05 \, \text{m} \)
- Area of the Square: \( A = (0.05)^2 = 0.0025 \, \text{m}^2 \)
- Area of the Circle: \( A = 0.0025 \, \text{m}^2 \)
- Radius of the Circle: \( r = \sqrt{\frac{0.0025}{\pi}} \approx 0.0282 \, \text{m} \)
- Convert: \( A = 25 \, \text{cm}^2 \), \( r \approx 2.82 \, \text{cm} \)

5. Frequently Asked Questions (FAQ)

Q: What is the largest square that can fit inside a circle?
A: The largest square that can fit inside a circle has a diagonal equal to the diameter of the circle, so its side length is \( s = r \times \sqrt{2} \), where \( r \) is the radius of the circle.

Q: What is the largest circle that can fit inside a square?
A: The largest circle that can fit inside a square has a diameter equal to the side of the square, so its radius is \( r = \frac{s}{2} \), where \( s \) is the side length of the square.