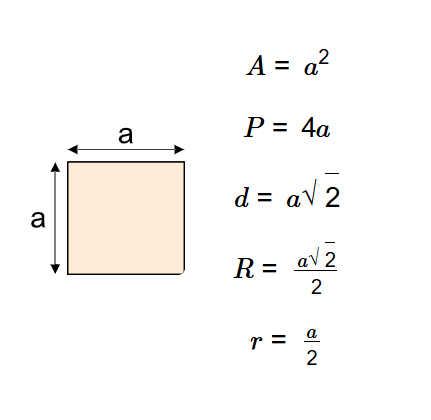Area of a Square Calculator

Area:

Perimeter:

Diagonal:

Circumradius:

Inradius:

1. What is a Square Area Calculator?

Definition: This calculator computes the area, perimeter, diagonal, circumradius, and inradius of a square given its side length \( a \). A square is a four-sided polygon with equal sides and right angles. The calculator supports length units (mm, cm, m, in, ft, yd) and area units (mm², cm², m², in², ft², yd²), defaulting to m for inputs and lengths, and m² for area.

Purpose: It aids in geometry education and practical applications by calculating key properties of squares, useful in fields like architecture, design, and engineering for creating or analyzing square shapes.

2. How Does the Calculator Work?

The calculator uses the following formulas for a square with side length \( a \):

Area: \( A = a^2 \)
Perimeter: \( P = 4a \)
Diagonal: \( d = a \sqrt{2} \)
Circumradius: \( R = \frac{a \sqrt{2}}{2} \)
Inradius: \( r = \frac{a}{2} \)

Steps:

Input the side length \( a \), with the unit defaulting to m.
Select the desired output units for area, perimeter, diagonal, circumradius, and inradius (defaulting to m² for area, m for lengths).
Validate input: ensure \( a > 0 \).
Convert the side length to meters for calculation.
Compute the area, perimeter, diagonal, circumradius, and inradius using the formulas above.
Convert the results to the selected units.
Display results with lengths and area to 4 decimal places.

3. Importance of Square Area Calculations

Square area calculations are essential for:

Geometry: Understanding the properties of squares, which are fundamental shapes in mathematics.
Construction: Calculating the area of square plots or tiles, often requiring unit conversions (e.g., m² to ft²).
Design: Creating patterns or layouts with square elements, where properties like the diagonal or circumradius are useful.

4. Using the Calculator

Examples:

Example 1: Side \( a = 2 \) m, Outputs in m², m
Area: \( A = 2^2 = 4.0000 \) m²
Perimeter: \( P = 4 \cdot 2 = 8.0000 \) m
Diagonal: \( d = 2 \cdot \sqrt{2} \approx 2.8284 \) m
Circumradius: \( R = \frac{2 \cdot \sqrt{2}}{2} \approx 1.4142 \) m
Inradius: \( r = \frac{2}{2} = 1.0000 \) m.
Example 2: Side \( a = 50 \) cm, Area in cm², Perimeter in mm, Diagonal in cm, Radii in mm
Convert to meters: \( a = 0.5 \) m
Area: \( A = 0.5^2 = 0.2500 \) m² = 2500.0000 cm²
Perimeter: \( P = 4 \cdot 0.5 = 2.0000 \) m = 2000.0000 mm
Diagonal: \( d = 0.5 \cdot \sqrt{2} \approx 0.7071 \) m = 70.7107 cm
Circumradius: \( R = \frac{0.7071}{2} \approx 0.3536 \) m = 353.5534 mm
Inradius: \( r = \frac{0.5}{2} = 0.2500 \) m = 250.0000 mm.
Example 3: Side \( a = 3 \) ft, Outputs in ft², ft
Convert to meters: \( a = 3 \cdot 0.3048 = 0.9144 \) m
Area: \( A = 0.9144^2 \approx 0.8361 \) m² = 9.0000 ft²
Perimeter: \( P = 4 \cdot 0.9144 \approx 3.6576 \) m = 12.0000 ft
Diagonal: \( d = 0.9144 \cdot \sqrt{2} \approx 1.2932 \) m = 4.2426 ft
Circumradius: \( R = \frac{1.2932}{2} \approx 0.6466 \) m = 2.1213 ft
Inradius: \( r = \frac{0.9144}{2} \approx 0.4572 \) m = 1.5000 ft.

5. Frequently Asked Questions (FAQ)

Q: What is a square?
A: A square is a four-sided polygon with equal sides and right angles (90°), making it a special type of rectangle and a regular polygon.

Q: Why do inputs and outputs default to m and m²?
A: Meters (m) and square meters (m²) are the default units to provide a standard metric base, ensuring consistency in calculations, but you can convert to other units as needed.

Q: What are the circumradius and inradius of a square?
A: The circumradius is the radius of the circle passing through all vertices (half the diagonal), and the inradius is the radius of the circle inscribed within the square (half the side length).