Slope Calculator with Multiple Points

Point 1:

x1: y1:

Point 2:

x2: y2: [Remove]

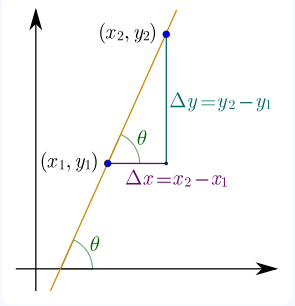
1. What is a Multi-Point Slope Calculator?

Definition: This calculator analyzes multiple points to determine the best-fit line using the least squares method. It calculates the slope (m), y-intercept, angle of inclination (θ), percentage grade, total distance, and pairwise distances, Δx, and Δy between consecutive points.

Purpose: It is used in mathematics, engineering, and data analysis to model linear trends and calculate distances along a path defined by multiple points.

2. How Does the Calculator Work?

The calculator uses the least squares method to fit a line to the points and computes additional properties:

Slope (m):

\( m = \frac{n \sum (x_i y_i) - \sum x_i \sum y_i}{n \sum (x_i^2) - (\sum x_i)^2} \)

Y-intercept (b):

\( b = \frac{\sum y_i - m \sum x_i}{n} \)

Angle (θ, degrees):

\( \theta = \arctan(m) \times \frac{180}{\pi} \)

Percentage Grade (%):

\( \text{Percentage Grade} = m \times 100 \)

Distance Between Consecutive Points (d):

\( d = \sqrt{(x_{i+1} - x_i)^2 + (y_{i+1} - y_i)^2} \)

Distance between x's (Δx) and y's (Δy):

\( \Delta x = x_{i+1} - x_i \quad \text{and} \quad \Delta y = y_{i+1} - y_i \)

Total Distance: Sum of distances between consecutive points.

Steps:

Enter the coordinates of at least two points.
Add or remove points as needed using the buttons.
Validate the inputs to ensure at least two points and no vertical line (all x values equal).
Fit a line using the least squares method to calculate slope and y-intercept.
Compute the angle, percentage grade, and distances using the formulas above.
Display the results with appropriate precision (4 decimal places for angle, percentage grade, and distances).

3. Importance of Multi-Point Slope Calculation

Multi-point slope calculations are essential for:

Data Analysis: Fitting a trend line to scattered data points.
Engineering: Designing paths or trajectories with multiple waypoints.
Surveying: Calculating distances and slopes across multiple survey points.

4. Using the Calculator

Example 1: Calculate the properties for points (0, 0), (1, 1), and (2, 2):

Points: (0, 0), (1, 1), (2, 2)
Least Squares Fit: Perfect line, Slope \( m = 1 \), Y-intercept \( b = 0 \)
Angle: \( \theta = \arctan(1) \times \frac{180}{\pi} = 45.0000^\circ \)
Percentage Grade: \( 1 \times 100 = 100.0000\% \)
Point 1 to Point 2: Distance \( \sqrt{(1-0)^2 + (1-0)^2} = 1.4142 \), Δx = 1, Δy = 1
Point 2 to Point 3: Distance \( \sqrt{(2-1)^2 + (2-1)^2} = 1.4142 \), Δx = 1, Δy = 1
Total Distance: \( 1.4142 + 1.4142 = 2.8284 \)

Example 2: Calculate the properties for points (1, 2), (3, 4), (5, 5):

Points: (1, 2), (3, 4), (5, 5)
Least Squares Fit: Slope \( m \approx 0.65 \), Y-intercept \( b \approx 1.45 \)
Angle: \( \theta = \arctan(0.65) \times \frac{180}{\pi} \approx 33.0243^\circ \)
Percentage Grade: \( 0.65 \times 100 \approx 65.0000\% \)
Point 1 to Point 2: Distance \( \sqrt{(3-1)^2 + (4-2)^2} = 2.8284 \), Δx = 2, Δy = 2
Point 2 to Point 3: Distance \( \sqrt{(5-3)^2 + (5-4)^2} = 2.2361 \), Δx = 2, Δy = 1
Total Distance: \( 2.8284 + 2.2361 = 5.0645 \)

5. Frequently Asked Questions (FAQ)

Q: Why use least squares for multiple points?
A: Least squares minimizes the error between the points and the fitted line, providing the best linear approximation.

Q: What happens if all x values are the same?
A: The slope becomes undefined (vertical line), and the calculator will display an error message.

Q: Can I calculate distances for non-consecutive points?
A: This calculator computes distances between consecutive points. For non-consecutive distances, you can calculate each pair separately.