Slant Height Calculator - Cone, Prism, Triangle

Shape Type:

Height \( h \):

Base radius \( r \):

1. What is a Slant Height Calculator?

Definition: This calculator computes the slant height for three geometric shapes: a right circular cone, a right angle prism, or a right triangle. The slant height is the distance along a slanted surface or hypotenuse, calculated from specific dimensions (height and base measurements) provided by the user.

Purpose: It assists in geometry education, engineering, and design by determining key distances for conical, prismatic, or triangular structures, such as roofs, supports, or slopes.

2. How Does the Calculator Work?

The calculator uses the following formulas based on the selected shape:

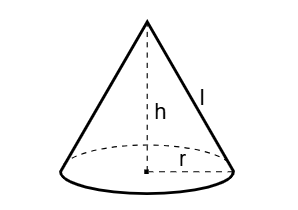
Right Circular Cone: Slant height \( l = \sqrt{r^2 + h^2} \), where \( r \) is the base radius and \( h \) is the height.
Right Angle Prism: Slant height \( l = \sqrt{b^2 + h^2} \), where \( b \) is the base edge length and \( h \) is the height.
Right Triangle: Slant height or hypotenuse \( c = \sqrt{a^2 + b^2} \), where \( a \) and \( b \) are the legs.

Unit Conversions:

Length Units: m, cm (1 m = 100 cm), mm (1 m = 1000 mm), in (1 m = 39.3701 in), ft (1 m = 3.28084 ft), yd (1 m = 1.09361 yd).

Steps:

Select the shape type (Cone, Prism, or Triangle).
Input the required dimensions (e.g., height and base radius for a cone) and select their units.
Validate inputs (must be positive).
Convert inputs to meters for calculations.
Compute the slant height using the appropriate formula.
Convert the output to the selected unit and format to 4 decimal places or scientific notation for small values.

3. Importance of Slant Height Calculations

Calculating slant heights is crucial for:

Geometry Education: Understanding the properties of cones, prisms, and triangles.
Architecture and Engineering: Designing structures like conical roofs, prismatic supports, or triangular frames.
Construction: Determining material lengths for slanted surfaces or supports.

4. Using the Calculator

Examples:

Example 1: Right Circular Cone
Inputs: Height \( h = 8 \, \text{cm} \), Base radius \( r = 6 \, \text{cm} \)
Convert: \( h = 0.08 \, \text{m} \), \( r = 0.06 \, \text{m} \)
Slant height: \( l = \sqrt{0.06^2 + 0.08^2} \approx 0.1 \, \text{m} = 10.0000 \, \text{cm} \).
Example 2: Right Angle Prism
Inputs: Height \( h = 3 \, \text{m} \), Base edge \( b = 4 \, \text{m} \)
Slant height: \( l = \sqrt{4^2 + 3^2} = 5 \, \text{m} \).
Example 3: Right Triangle
Inputs: Height \( a = 5 \, \text{cm} \), Base \( b = 12 \, \text{cm} \)
Convert: \( a = 0.05 \, \text{m} \), \( b = 0.12 \, \text{m} \)
Hypotenuse: \( c = \sqrt{0.05^2 + 0.12^2} \approx 0.13 \, \text{m} = 13.0000 \, \text{cm} \).

5. Frequently Asked Questions (FAQ)

Q: What is a slant height?
A: The slant height is the distance along a slanted surface, such as from the apex to the base edge in a cone or prism, or the hypotenuse in a right triangle.

Q: Why are the formulas similar for all three shapes?
A: Each shape involves a right triangle where the slant height is the hypotenuse, with the legs being the height and a base dimension, leading to the Pythagorean theorem.

Q: What is a right angle prism in this context?
A: It refers to a prism with a right angle, typically with a square or rectangular base, where the slant height is the diagonal edge from a base corner to the top.