Reference Angle Calculator

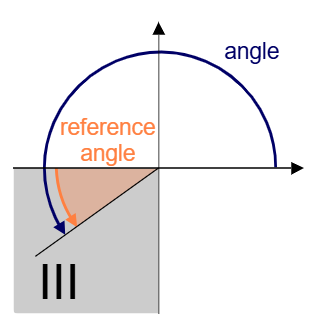
1. What is a Reference Angle Calculator?

Definition: This calculator computes the reference angle for a given angle, which is the acute angle (0° to 90° or 0 to π/2 radians) formed between the terminal side of the angle and the x-axis in standard position.

Purpose: It simplifies trigonometric calculations by reducing any angle to its equivalent acute angle in the first quadrant, useful in mathematics, physics, and engineering.

2. How Does the Calculator Work?

The calculator uses the following steps:

Normalize the Angle:
- Degrees: \( \theta = \theta \mod 360^\circ \).
- Radians: \( \theta = \theta \mod 2\pi \).
Determine the Quadrant and Calculate Reference Angle:
- First Quadrant (0° ≤ θ < 90° or 0 ≤ θ < π/2): \( \theta_{\text{ref}} = \theta \).
- Second Quadrant (90° ≤ θ < 180° or π/2 ≤ θ < π): \( \theta_{\text{ref}} = 180^\circ - \theta \) (or \( \pi - \theta \)).
- Third Quadrant (180° ≤ θ < 270° or π ≤ θ < 3π/2): \( \theta_{\text{ref}} = \theta - 180^\circ \) (or \( \theta - \pi \)).
- Fourth Quadrant (270° ≤ θ < 360° or 3π/2 ≤ θ < 2π): \( \theta_{\text{ref}} = 360^\circ - \theta \) (or \( 2\pi - \theta \)).
Unit Conversion:
- Degrees to radians: \( \text{radians} = \text{degrees} \times \frac{\pi}{180} \).
- Radians to degrees: \( \text{degrees} = \text{radians} \times \frac{180}{\pi} \).

Steps:

Input the angle \( \theta \) and select its unit (degrees or radians).
Validate the input (must be positive).
Convert the angle to degrees for processing.
Normalize the angle to 0°–360°.
Calculate the reference angle based on the quadrant.
Convert the reference angle to the selected output unit (degrees or radians).
Format the output to 4 decimal places or scientific notation for small values.

3. Importance of Reference Angle Calculations

Calculating reference angles is crucial for:

Trigonometry: Simplifying sine, cosine, and tangent calculations by using acute angles.
Geometry Education: Understanding angle relationships in the coordinate plane.
Physics and Engineering: Analyzing angles in rotational motion or wave functions.

4. Using the Calculator

Examples:

Example 1: Angle \( \theta = 150^\circ \)
- Normalize: \( 150^\circ \mod 360^\circ = 150^\circ \).
- Quadrant: Second (90° ≤ 150° < 180°).
- Reference Angle: \( \theta_{\text{ref}} = 180^\circ - 150^\circ = 30^\circ = 0.5236 \, \text{rad} \).
Example 2: Angle \( \theta = 5\pi/3 \, \text{rad} \)
- Convert: \( \frac{5\pi}{3} \times \frac{180}{\pi} = 300^\circ \).
- Normalize: \( 300^\circ \mod 360^\circ = 300^\circ \).
- Quadrant: Fourth (270° ≤ 300° < 360°).
- Reference Angle: \( \theta_{\text{ref}} = 360^\circ - 300^\circ = 60^\circ = \frac{\pi}{3} \approx 1.0472 \, \text{rad} \).

5. Frequently Asked Questions (FAQ)

Q: What is a reference angle?
A: A reference angle is the acute angle (0° to 90° or 0 to π/2 radians) formed between the terminal side of an angle in standard position and the x-axis. It is always positive and simplifies trigonometric calculations.

Q: Why is the reference angle always acute?
A: The reference angle is defined as the smallest angle to the x-axis, ensuring it is between 0° and 90° (or 0 and π/2 radians), making it easier to evaluate trigonometric functions.