Rectangle Perimeter and Area Calculator

Perimeter:

Area:

square

Diagonal (d):

Circumcircle Radius:

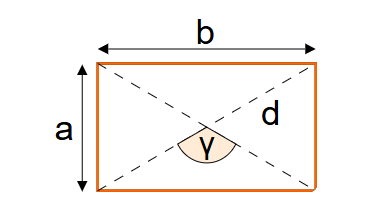
1. What is the Rectangle Properties Calculator?

Definition: The Rectangle Properties Calculator computes the perimeter, area, diagonal, angle between diagonals, and circumcircle radius of a rectangle based on its width and length.

Purpose: Assists in calculating geometric properties for construction, design, or educational purposes with customizable units.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Perimeter:

\[ P = 2 \times (a + b) \]

Area:

\[ A = a \times b \]

Diagonal:

\[ d = \sqrt{a^2 + b^2} \]

Angle between Diagonals:

\[ \gamma = 90^\circ \]

(The diagonals of a rectangle intersect at 90° at the center, with no obtuse angle formed due to the rectangle's right-angled nature.)

Circumcircle Radius:

\[ r = \frac{d}{2} \]

Where:

\( a \): Width.
\( b \): Length.
\( P \): Perimeter.
\( A \): Area.
\( d \): Diagonal.
\( r \): Circumcircle radius.

Steps:

Step 1: Input Width and Length. Enter positive values for width (a) and length (b).
Step 2: Select Unit. Choose from cm, m, inch, feet, or yard.
Step 3: Calculate. Compute all properties with fixed 4 decimal place precision.

3. Importance of Rectangle Property Calculation

Calculating rectangle properties is crucial for:

Construction: Estimating materials for frames or floors.
Design: Planning rectangular layouts or spaces.
Education: Teaching geometry and spatial relationships.

4. Using the Calculator

Example 1: Width 14 cm, Length 10 cm:

Step 1: Width = 14 cm, Length = 10 cm.
Step 2: Perimeter = \( 2 \times (14 + 10) = 48 \) cm.
Step 3: Area = \( 14 \times 10 = 140 \) square cm.
Step 4: Diagonal = \( \sqrt{14^2 + 10^2} \approx 17.2047 \) cm.
Step 5: Circumcircle Radius = \( 17.2047 / 2 \approx 8.6024 \) cm.
Result: Perimeter = 48.0000 cm, Area = 140.0000 square cm, Diagonal = 17.2047 cm, Angle = 90°, Circumcircle Radius = 8.6024 cm.

Example 2: Width 5 inches, Length 3 inches:

Step 1: Width = 5 inches, Length = 3 inches.
Step 2: Perimeter = \( 2 \times (5 + 3) = 16 \) inches.
Step 3: Area = \( 5 \times 3 = 15 \) square inches.
Step 4: Diagonal = \( \sqrt{5^2 + 3^2} \approx 5.8309 \) inches.
Step 5: Circumcircle Radius = \( 5.8309 / 2 \approx 2.9155 \) inches.
Result: Perimeter = 16.0000 inches, Area = 15.0000 square inches, Diagonal = 5.8309 inches, Angle = 90°, Circumcircle Radius = 2.9155 inches.

Example 3: Width 2 m, Length 1.5 m:

Step 1: Width = 2 m, Length = 1.5 m.
Step 2: Perimeter = \( 2 \times (2 + 1.5) = 7 \) m.
Step 3: Area = \( 2 \times 1.5 = 3 \) square m.
Step 4: Diagonal = \( \sqrt{2^2 + 1.5^2} \approx 2.5000 \) m.
Step 5: Circumcircle Radius = \( 2.5000 / 2 = 1.2500 \) m.
Result: Perimeter = 7.0000 m, Area = 3.0000 square m, Diagonal = 2.5000 m, Angle = 90°, Circumcircle Radius = 1.2500 m.

Example 4: Width 3 feet, Length 2 feet:

Step 1: Width = 3 feet, Length = 2 feet.
Step 2: Perimeter = \( 2 \times (3 + 2) = 10 \) feet.
Step 3: Area = \( 3 \times 2 = 6 \) square feet.
Step 4: Diagonal = \( \sqrt{3^2 + 2^2} \approx 3.6056 \) feet.
Step 5: Circumcircle Radius = \( 3.6056 / 2 \approx 1.8028 \) feet.
Result: Perimeter = 10.0000 feet, Area = 6.0000 square feet, Diagonal = 3.6056 feet, Angle = 90°, Circumcircle Radius = 1.8028 feet.

5. Frequently Asked Questions (FAQ)

Q: What is a rectangle?
A: A rectangle is a four-sided polygon with opposite sides equal and all angles 90°.

Q: Why is the angle between diagonals 90°?
A: The diagonals of a rectangle bisect each other at 90° due to the right-angled nature of the shape.

Q: What is the circumcircle radius?
A: It’s the radius of the circle passing through all four vertices, equal to half the diagonal.