Rectangle Calculator - Find Area, Perimeter, and Diagonal

Area:

Perimeter:

Diagonal:

1. What is a Rectangle Calculator?

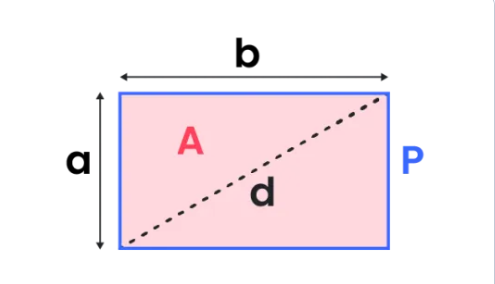
Definition: This calculator computes the area, perimeter, and diagonal of a rectangle using its length (\( l \)) and width (\( w \)). A rectangle is a quadrilateral with opposite sides equal and all angles equal to 90°.

Purpose: It supports geometry education, architectural design, and engineering by calculating key parameters for rectangular shapes, such as floors, walls, or panels.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Area: \( A = l \cdot w \).
Perimeter: \( P = 2 \cdot (l + w) \).
Diagonal: \( d = \sqrt{l^2 + w^2} \).

Unit Conversions:

Length Units: m, cm (1 m = 100 cm), mm (1 m = 1000 mm), in (1 m = 39.3701 in), ft (1 m = 3.28084 ft), yd (1 m = 1.09361 yd).
Area Units: m², cm² (1 m² = 10000 cm²), mm² (1 m² = 1000000 mm²), in² (1 m² = 1550.0031 in²), ft² (1 m² = 10.7639 ft²), yd² (1 m² = 1.19599 yd²).

Steps:

Input the length \( l \) and width \( w \), selecting their units.
Validate inputs: Length and width must be positive.
Convert inputs to meters for calculations.
Compute the area, perimeter, and diagonal using the formulas above.
Convert outputs to the selected units.
Format outputs to 4 decimal places or scientific notation for small values.

3. Importance of Rectangle Calculations

Calculating the properties of a rectangle is crucial for:

Geometry Education: Understanding basic properties of quadrilaterals and the Pythagorean theorem.
Construction and Architecture: Determining material requirements for rectangular surfaces, such as flooring, tiling, or wall coverings.
Engineering: Analyzing structural components with rectangular shapes in design and manufacturing.

4. Using the Calculator

Examples:

Example 1: Length \( l = 5 \, \text{cm} \), Width \( w = 3 \, \text{cm} \)
- Convert: \( l = 0.05 \, \text{m} \), \( w = 0.03 \, \text{m} \).
- Area: \( A = 0.05 \cdot 0.03 = 0.0015 \, \text{m}^2 = 15.0000 \, \text{cm}^2 \).
- Perimeter: \( P = 2 \cdot (0.05 + 0.03) = 0.16 \, \text{m} = 16.0000 \, \text{cm} \).
- Diagonal: \( d = \sqrt{0.05^2 + 0.03^2} \approx 0.0583 \, \text{m} = 5.8310 \, \text{cm} \).
Example 2: Length \( l = 4 \, \text{m} \), Width \( w = 2 \, \text{m} \)
- Area: \( A = 4 \cdot 2 = 8.0000 \, \text{m}^2 \).
- Perimeter: \( P = 2 \cdot (4 + 2) = 12.0000 \, \text{m} \).
- Diagonal: \( d = \sqrt{4^2 + 2^2} \approx 4.4721 \, \text{m} \).

5. Frequently Asked Questions (FAQ)

Q: What is a rectangle?
A: A rectangle is a quadrilateral with opposite sides equal and parallel, and all angles equal to 90°. If length equals width, it is a square.

Q: How is the diagonal calculated?
A: The diagonal is calculated using the Pythagorean theorem, as the diagonal forms the hypotenuse of a right triangle with the length and width as legs.

Q: Can the calculator handle different units?
A: Yes, the calculator supports inputs and outputs in meters, centimeters, millimeters, inches, feet, and yards, with automatic conversions.