1. What is a Quarter Circle Calculator?
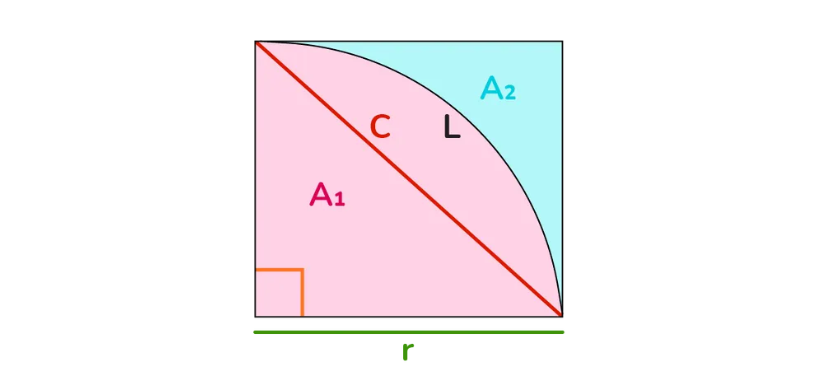
Definition: This calculator computes the chord (\( c \)), quarter arc (\( L \)), perimeter, quarter area (\( A_1 \)), and external area (\( A_2 \)) of a quarter circle, which is one-fourth of a full circle defined by a radius (\( r \)) and a 90° central angle.
Purpose: It aids in geometry education, engineering, and design by calculating key parameters for applications like architecture, manufacturing, and road design where quarter circles are common.
2. How Does the Calculator Work?
The calculator takes the radius (\( r \)) and a unit (m, cm, mm, in, ft, yd) and computes:
- Chord (\( c \)):
- Formula: \( c = 2 \times r \times \sin\left(\frac{90^\circ}{2}\right) \approx 1.4142 \times r \).
- The chord is the line segment connecting the two radii, forming the hypotenuse of a right-angled triangle.
- Quarter Arc (\( L \)):
- Formula: \( L = \frac{\pi r}{2} \).
- The arc is one-fourth of the circle’s circumference.
- Perimeter:
- Formula: \( P = \frac{\pi r}{2} + 2r \).
- Sum of the quarter arc and two radii.
- Quarter Area (\( A_1 \)):
- Formula: \( A_1 = \frac{\pi r^2}{4} \).
- One-fourth of the full circle’s area.
- External Area (\( A_2 \)):
- Formula: \( A_2 = r^2 - \frac{\pi r^2}{4} \).
- Area of the square (side \( r \)) minus the quarter circle area.
Unit Conversions:
- Length Units: m, cm (1 m = 100 cm), mm (1 m = 1000 mm), in (1 m = 39.3701 in), ft诞(1 m = 3.28084 ft), yd (1 m = 1.09361 yd).
- Area Units: m², cm² (1 m² = 10000 cm²), mm² (1 m² = 1000000 mm²), in² (1 m² = 1550.0031 in²), ft² (1 m² = 10.7639 ft²), yd² (1 m² = 1.19599 yd²).
Steps:
- Input the radius (\( r \)) and select a unit.
- Validate input (\( r > 0 \)).
- Convert radius to meters for calculations.
- Compute chord, quarter arc, perimeter, quarter area, and external area.
- Convert results back to the selected unit and format to 4 decimal places or scientific notation for small values.
3. Importance of Quarter Circle Calculations
Calculating quarter circle parameters is crucial for:
- Geometry Education: Understanding circular sectors and their properties.
- Engineering and Manufacturing: Designing curved parts, molds, or templates.
- Architecture and Road Design: Creating roundabouts, curved roadways, or quarter-circle structures.
4. Using the Calculator
Examples:
- Example 1: Radius \( r = 6 \, \text{cm} \)
Convert: \( r = 0.06 \, \text{m} \).
Chord: \( c = 2 \times 0.06 \times \sin(\pi/4) \approx 0.0849 \, \text{m} = 8.4853 \, \text{cm} \).
Quarter Arc: \( L = \frac{\pi \times 0.06}{2} \approx 0.0942 \, \text{m} = 9.4248 \, \text{cm} \).
Perimeter: \( P = 0.0942 + 2 \times 0.06 \approx 0.2142 \, \text{m} = 21.4248 \, \text{cm} \).
Quarter Area: \( A_1 = \frac{\pi \times 0.06^2}{4} \approx 0.0028 \, \text{m}^2 = 28.2743 \, \text{cm}^2 \).
External Area: \( A_2 = 0.06^2 - 0.0028 \approx 0.0008 \, \text{m}^2 = 7.7257 \, \text{cm}^2 \).
- Example 2: Radius \( r = 2 \, \text{m} \)
Chord: \( c = 2 \times 2 \times \sin(\pi/4) \approx 2.8284 \, \text{m} \).
Quarter Arc: \( L = \frac{\pi \times 2}{2} \approx 3.1416 \, \text{m} \).
Perimeter: \( P = 3.1416 + 2 \times 2 \approx 7.1416 \, \text{m} \).
Quarter Area: \( A_1 = \frac{\pi \times 2^2}{4} \approx 3.1416 \, \text{m}^2 \).
External Area: \( A_2 = 2^2 - 3.1416 \approx 0.8584 \, \text{m}^2 \).
- Example 3: Radius \( r = 10 \, \text{in} \)
Convert: \( r = 0.254 \, \text{m} \).
Chord: \( c \approx 0.3598 \, \text{m} = 14.1667 \, \text{in} \).
Quarter Arc: \( L \approx 0.3991 \, \text{m} = 15.7146 \, \text{in} \).
Perimeter: \( P \approx 0.9071 \, \text{m} = 35.7146 \, \text{in} \).
Quarter Area: \( A_1 \approx 0.0507 \, \text{m}^2 = 78.5398 \, \text{in}^2 \).
External Area: \( A_2 \approx 0.0137 \, \text{m}^2 = 21.4602 \, \text{in}^2 \).
5. Frequently Asked Questions (FAQ)
Q: What is a quarter circle?
A: A quarter circle is one-fourth of a full circle, formed by two perpendicular radii and a 90° arc, resembling a quadrant or a slice of pie.
Q: What is the external area of a quarter circle?
A: The external area is the area of a square with side length equal to the radius minus the quarter circle’s area, representing the region outside the quarter circle but within the square.
Q: Why is the chord calculated using the sine function?
A: The chord forms the hypotenuse of a right-angled triangle within the quarter circle. The sine of half the central angle (45°) is used to compute the chord length relative to the radius.
 Home
Home
 Back
Back