Power of 10 Calculator

1. What is a Power of 10 Calculator?

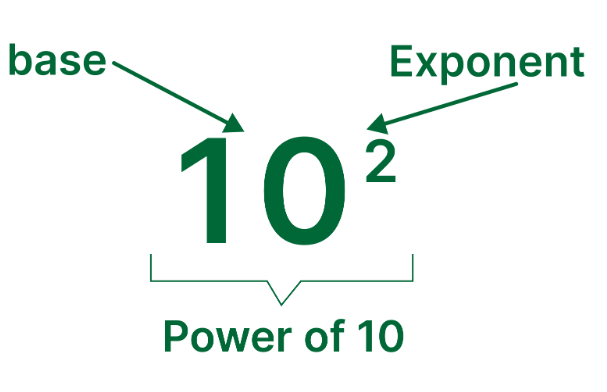
Definition: This calculator computes the result of 10 raised to any real number exponent (\( 10^n \)), where \( n \) can be positive, negative, or a decimal. The power of 10 represents 10 multiplied by itself \( n \) times for positive integer \( n \), the reciprocal for negative \( n \), or a fractional power for decimal \( n \).

Purpose: It aids in mathematics, science, and engineering by simplifying calculations involving very large or very small numbers, such as in scientific notation, computer science, and financial modeling.

2. How Does the Calculator Work?

The calculator takes the exponent (\( n \)) and computes:

Power of 10 (\( 10^n \)):
- Formula: \( 10^n \), where \( n \) is a real number.
- For positive integer \( n \): \( 10^n = 10 \times 10 \times \ldots \times 10 \) (\( n \) times).
- For negative \( n \): \( 10^{-n} = \frac{1}{10^n} \).
- For decimal \( n \): \( 10^n \) represents a fractional power, e.g., \( 10^{0.5} = \sqrt{10} \).
- For \( n = 0 \): \( 10^0 = 1 \).

Steps:

Input the exponent (\( n \)), which can be any real number.
Compute \( 10^n \) using the power function.
Display the result, formatted to 4 decimal places or scientific notation for small values.

3. Importance of Power of 10 Calculations

Calculating powers of 10 is crucial for:

Scientific Notation: Simplifying the representation of large or small numbers, e.g., \( 1.23 \times 10^4 \).
Engineering and Physics: Handling measurements like distances, masses, or frequencies (e.g., \( 1.988 \times 10^{30} \) kg for the Sun’s mass).
Computer Science: Working with data storage units like Megabytes (\( 10^6 \)) or Gigabytes (\( 10^9 \)).

4. Using the Calculator

Examples:

Example 1: Exponent \( n = 3 \)
Power of 10: \( 10^3 = 10 \times 10 \times 10 = 1000.0000 \).
Example 2: Exponent \( n = -2.5 \)
Power of 10: \( 10^{-2.5} = \frac{1}{10^{2.5}} \approx 0.0032 \).
Example 3: Exponent \( n = 1.235 \)
Power of 10: \( 10^{1.235} \approx 17.1828 \).

5. Frequently Asked Questions (FAQ)

Q: What is a power of 10?
A: A power of 10 is 10 raised to a real number exponent, representing 10 multiplied by itself for positive integers, its reciprocal for negative exponents, or a fractional power for decimal exponents.

Q: Can the exponent be a decimal number?
A: Yes, the calculator allows decimal exponents, which result in fractional powers of 10. For example, \( 10^{0.5} \) equals the square root of 10, approximately 3.1623.

Q: How are negative exponents handled?
A: A negative exponent \( n \) results in a value of one divided by 10 raised to the positive exponent, producing a decimal value. For example, \( 10^{-3} \) equals 0.001.