Polygon Angle Calculator

1. What is a Polygon Angle Calculator?

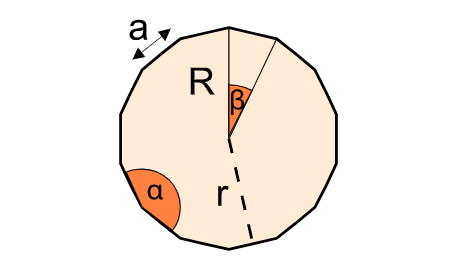
Definition: This calculator computes the interior angle (\( \alpha \)) and exterior angle (\( \beta \)) of a regular polygon based on the number of sides (\( n \)). A regular polygon has all sides and angles equal.

Purpose: It aids in geometry education, architecture, and design by calculating angles for regular polygons, useful in applications like tiling, computer graphics, and structural engineering.

2. How Does the Calculator Work?

The calculator takes the number of sides (\( n \)) of a regular polygon and computes:

Interior Angle (\( \alpha \)):
- Formula: \( \alpha = \frac{(n - 2) \times 180}{n} \).
Exterior Angle (\( \beta \)):
- Formula: \( \beta = \frac{360}{n} \).

Steps:

Input the number of sides (\( n \)).
Validate input (\( n \geq 3 \), integer).
Compute the interior angle using the formula for the sum of interior angles divided by the number of sides.
Compute the exterior angle by dividing 360° by the number of sides.
Display results in degrees, formatted to 4 decimal places or scientific notation for small values.

3. Importance of Polygon Angle Calculations

Calculating polygon angles is crucial for:

Geometry Education: Understanding properties of regular polygons.
Architecture and Design: Creating patterns, such as tiles or mosaics, that rely on regular polygons.
Computer Graphics: Rendering shapes and calculating rotations in 3D modeling.

4. Using the Calculator

Examples:

Example 1: Number of sides \( n = 3 \) (Triangle)
Interior Angle: \( \alpha = \frac{(3 - 2) \times 180}{3} = 60.0000^\circ \).
Exterior Angle: \( \beta = \frac{360}{3} = 120.0000^\circ \).
Example 2: Number of sides \( n = 5 \) (Pentagon)
Interior Angle: \( \alpha = \frac{(5 - 2) \times 180}{5} = 108.0000^\circ \).
Exterior Angle: \( \beta = \frac{360}{5} = 72.0000^\circ \).
Example 3: Number of sides \( n = 8 \) (Octagon)
Interior Angle: \( \alpha = \frac{(8 - 2) \times 180}{8} = 135.0000^\circ \).
Exterior Angle: \( \beta = \frac{360}{8} = 45.0000^\circ \).

5. Frequently Asked Questions (FAQ)

Q: What is a regular polygon?
A: A regular polygon is a polygon with all sides and all angles equal, such as an equilateral triangle, square, or regular pentagon.

Q: Why must the number of sides be at least 3?
A: A polygon requires at least three sides to form a closed shape. Fewer than three sides cannot create a polygon.

Q: How are interior and exterior angles related?
A: For any regular polygon, the interior angle (\( \alpha \)) and exterior angle (\( \beta \)) are supplementary, meaning \( \alpha + \beta = 180^\circ \).