Polar Form Calculator

1. What is a Polar Form Calculator?

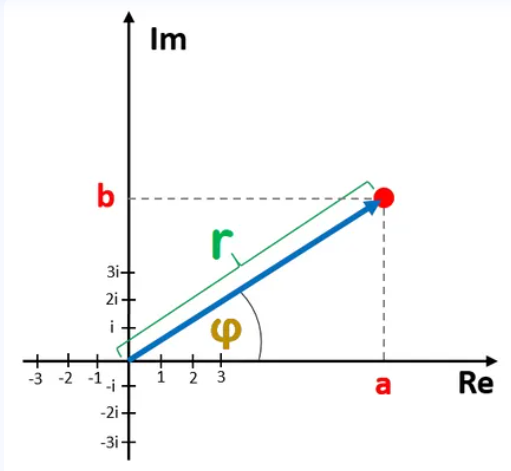
Definition: This calculator converts a complex number from rectangular form (\( a + bi \)) to polar form (\( r \angle \phi \)), where \( r \) is the magnitude and \( \phi \) is the phase angle in degrees.

Purpose: It aids in electrical engineering, signal processing, and mathematics by simplifying complex number operations, such as multiplication and division, which are easier in polar form.

2. How Does the Calculator Work?

The calculator takes the real part (\( a \)) and imaginary part (\( b \)) of a complex number and computes:

Magnitude (\( r \)):
- Formula: \( r = \sqrt{a^2 + b^2} \).
Phase (\( \phi \)):
- Formula: \( \phi = \text{atan2}(b, a) \), where atan2 is the two-argument arctangent function.
- Output in degrees, normalized to [0, 360).

Steps:

Input the real part (\( a \)) and imaginary part (\( b \)).
Validate inputs (not both zero).
Compute the magnitude using the Pythagorean theorem.
Compute the phase using atan2, convert to degrees, and normalize.
Display results formatted to 4 decimal places or scientific notation for small values.

3. Importance of Polar Form Calculations

Converting complex numbers to polar form is crucial for:

Electrical Engineering: Analyzing AC circuits, where impedance and phase are critical.
Signal Processing: Working with signals in the frequency domain, such as in Fourier transforms.
Mathematics: Simplifying operations like multiplication, division, and powers of complex numbers.

4. Using the Calculator

Examples:

Example 1: Real part \( a = 3 \), Imaginary part \( b = 4 \)
Magnitude: \( r = \sqrt{3^2 + 4^2} = \sqrt{25} = 5.0000 \).
Phase: \( \phi = \text{atan2}(4, 3) \approx 0.9273 \, \text{radians} = 53.1301^\circ \).
Result: \( 5 \angle 53.1301^\circ \).
Example 2: Real part \( a = -2 \), Imaginary part \( b = -2 \)
Magnitude: \( r = \sqrt{(-2)^2 + (-2)^2} = \sqrt{8} \approx 2.8284 \).
Phase: \( \phi = \text{atan2}(-2, -2) \approx -2.3562 \, \text{radians} \approx -135^\circ \), normalized to \( 225.0000^\circ \).
Result: \( 2.8284 \angle 225.0000^\circ \).
Example 3: Real part \( a = 1 \), Imaginary part \( b = 0 \)
Magnitude: \( r = \sqrt{1^2 + 0^2} = 1.0000 \).
Phase: \( \phi = \text{atan2}(0, 1) = 0^\circ \).
Result: \( 1 \angle 0^\circ \).

5. Frequently Asked Questions (FAQ)

Q: What is the polar form of a complex number?
A: The polar form expresses a complex number as \( r \angle \phi \), where \( r \) is the magnitude (distance from the origin) and \( \phi \) is the phase angle (angle from the positive real axis).

Q: Why use atan2 instead of regular arctangent?
A: The atan2 function considers the signs of both \( a \) and \( b \), correctly placing the angle in the appropriate quadrant, unlike regular arctangent, which has a limited range.

Q: What happens if both inputs are zero?
A: If both real and imaginary parts are zero, the complex number is at the origin, and the magnitude is zero. Since the phase is undefined, the calculator returns an error.