Perimeter of a Triangle with Vertices Calculator

Perimeter of a Triangle with Vertices Formula

Vertex 1 (x):

Vertex 1 (y):

Vertex 2 (x):

Vertex 2 (y):

Vertex 3 (x):

Vertex 3 (y):

Unit:

1. What is the Perimeter of a Triangle with Vertices Calculator?

Definition: The Perimeter of a Triangle with Vertices Calculator computes the perimeter of a triangle based on the coordinates of its three vertices using the distance formula.

Purpose: Assists in calculating the total boundary length of a triangle for geometry, design, or educational purposes with customizable units.

2. How Does the Calculator Work?

The calculator uses the following formula:

Perimeter Formula:

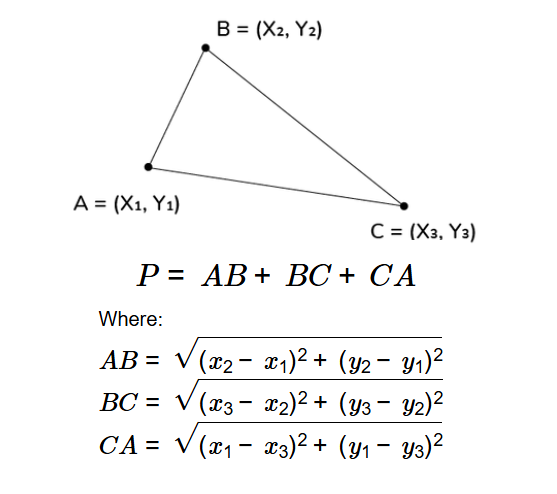
\[ P = AB + BC + CA \]

Where:

\( AB = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
\( BC = \sqrt{(x_3 - x_2)^2 + (y_3 - y_2)^2} \)
\( CA = \sqrt{(x_1 - x_3)^2 + (y_1 - y_3)^2} \)
\( (x_1, y_1), (x_2, y_2), (x_3, y_3) \): Coordinates of vertices \(A\), \(B\), and \(C\).
\( P \): Perimeter, adjusted by the selected unit.

Steps:

Step 1: Input Vertex Coordinates. Enter x and y values for all three vertices.
Step 2: Select Unit. Choose from cm, m, inch, feet, or yard.
Step 3: Calculate. Compute the perimeter with fixed 4 decimal place precision.

3. Importance of Triangle Perimeter Calculation with Vertices

Calculating the perimeter with vertex coordinates is crucial for:

Geometry: Analyzing triangle properties in coordinate systems.
Design: Planning triangular layouts or boundaries.
Education: Teaching coordinate geometry and distance calculations.

4. Using the Calculator

Example 1: Vertices A(-5, -2), B(-2, -2), C(-5, 2) in cm:

Step 1: Coordinates = (-5, -2), (-2, -2), (-5, 2).
Step 2: \( AB = \sqrt{(-2 - (-5))^2 + (-2 - (-2))^2} = \sqrt{3^2 + 0^2} = 3 \) cm.
Step 3: \( BC = \sqrt{(-5 - (-2))^2 + (2 - (-2))^2} = \sqrt{(-3)^2 + 4^2} = \sqrt{9 + 16} = 5 \) cm.
Step 4: \( CA = \sqrt{(-5 - (-5))^2 + (-2 - 2)^2} = \sqrt{0^2 + (-4)^2} = 4 \) cm.
Step 5: Perimeter = \( 3 + 5 + 4 = 12 \) cm.
Result: Perimeter = 12.0000 cm.

Example 2: Vertices A(0, 0), B(3, 0), C(0, 4) in inches:

Step 1: Coordinates = (0, 0), (3, 0), (0, 4).
Step 2: \( AB = \sqrt{(3 - 0)^2 + (0 - 0)^2} = 3 \) inches.
Step 3: \( BC = \sqrt{(0 - 3)^2 + (4 - 0)^2} = \sqrt{9 + 16} = 5 \) inches.
Step 4: \( CA = \sqrt{(0 - 0)^2 + (0 - 4)^2} = 4 \) inches.
Step 5: Perimeter = \( 3 + 5 + 4 = 12 \) inches.
Result: Perimeter = 12.0000 inches.

Example 3: Vertices A(1, 1), B(4, 1), C(1, 5) in m:

Step 1: Coordinates = (1, 1), (4, 1), (1, 5).
Step 2: \( AB = \sqrt{(4 - 1)^2 + (1 - 1)^2} = 3 \) m.
Step 3: \( BC = \sqrt{(1 - 4)^2 + (5 - 1)^2} = \sqrt{9 + 16} = 5 \) m.
Step 4: \( CA = \sqrt{(1 - 1)^2 + (1 - 5)^2} = 4 \) m.
Step 5: Perimeter = \( 3 + 5 + 4 = 12 \) m.
Result: Perimeter = 12.0000 m.

Example 4: Vertices A(-1, -1), B(2, -1), C(-1, 3) in feet:

Step 1: Coordinates = (-1, -1), (2, -1), (-1, 3).
Step 2: \( AB = \sqrt{(2 - (-1))^2 + (-1 - (-1))^2} = 3 \) feet.
Step 3: \( BC = \sqrt{(-1 - 2)^2 + (3 - (-1))^2} = \sqrt{9 + 16} = 5 \) feet.
Step 4: \( CA = \sqrt{(-1 - (-1))^2 + (-1 - 3)^2} = 4 \) feet.
Step 5: Perimeter = \( 3 + 5 + 4 = 12 \) feet.
Result: Perimeter = 12.0000 feet.

5. Frequently Asked Questions (FAQ)

Q: What is a triangle?
A: A triangle is a three-sided polygon with three vertices and three angles summing to 180°.

Q: How is the perimeter calculated with vertices?
A: The perimeter is the sum of the distances between consecutive vertices, computed using the distance formula.

Q: What if the vertices are collinear?
A: The calculator assumes a valid triangle; collinear points result in zero area, indicating an invalid triangle.