Perimeter of a Sector Calculator

Radius:

Angle Type:

Central Angle (0° to 360°):

Unit:

1. What is the Perimeter of a Sector Calculator?

Definition: The Perimeter of a Sector Calculator computes the perimeter and arc length of a sector of a circle by adding the lengths of the two radii and the arc length, based on the radius and central angle.

Purpose: Assists in calculating the boundary length of a sector for applications in geometry, design, or engineering with customizable units.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Perimeter Formula:

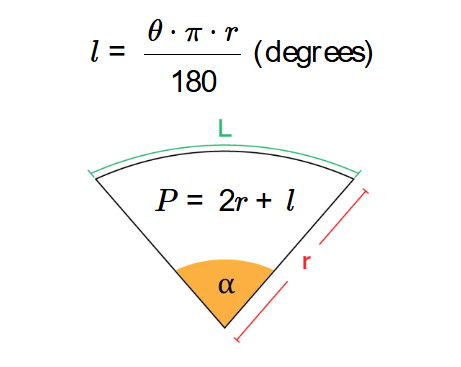
\[ P = 2r + l \]

Arc Length Formula:

\[ l = r \cdot \theta \text{ (radians)} \]

\[ l = \frac{\theta \cdot \pi \cdot r}{180} \text{ (degrees)} \]

Where:

\( r \): Radius of the circle.
\( \theta \): Central angle (in radians or degrees).
\( l \): Arc length.
\( P \): Perimeter, adjusted by the selected unit.

Steps:

Step 1: Input Radius. Enter a positive radius value.
Step 2: Select Angle Type. Choose degrees (0° to 360°) or radians (0 to 2π).
Step 3: Enter Central Angle. Provide the angle value.
Step 4: Select Unit. Choose from cm, m, inch, feet, or yard.
Step 5: Calculate. Compute the perimeter and arc length with fixed 4 decimal place precision.

3. Importance of Sector Perimeter and Arc Length Calculation

Calculating the perimeter and arc length of a sector is crucial for:

Design: Planning curved sections in architecture or graphics.
Education: Teaching circular geometry and arc measurements.
Manufacturing: Estimating material needs for sector-shaped components.

4. Using the Calculator

Example 1: Radius 8 cm, Angle 90°:

Step 1: Radius = 8 cm.
Step 2: Angle Type = Degrees, Angle = 90°.
Step 3: Arc Length = \( \frac{90 \cdot \pi \cdot 8}{180} \approx 12.5664 \) cm.
Step 4: Perimeter = \( 2 \cdot 8 + 12.5664 \approx 28.5664 \) cm.
Result: Perimeter = 28.5664 cm, Arc Length = 12.5664 cm.

Example 2: Radius 5 inches, Angle π/2 radians:

Step 1: Radius = 5 inches.
Step 2: Angle Type = Radians, Angle = π/2 ≈ 1.5708.
Step 3: Arc Length = \( 5 \cdot 1.5708 \approx 7.8540 \) inches.
Step 4: Perimeter = \( 2 \cdot 5 + 7.8540 \approx 17.8540 \) inches.
Result: Perimeter = 17.8540 inches, Arc Length = 7.8540 inches.

Example 3: Radius 2 m, Angle 60°:

Step 1: Radius = 2 m.
Step 2: Angle Type = Degrees, Angle = 60°.
Step 3: Arc Length = \( \frac{60 \cdot \pi \cdot 2}{180} \approx 2.0944 \) m.
Step 4: Perimeter = \( 2 \cdot 2 + 2.0944 \approx 6.0944 \) m.
Result: Perimeter = 6.0944 m, Arc Length = 2.0944 m.

Example 4: Radius 3 feet, Angle 2 radians:

Step 1: Radius = 3 feet.
Step 2: Angle Type = Radians, Angle = 2.
Step 3: Arc Length = \( 3 \cdot 2 \approx 6.0000 \) feet.
Step 4: Perimeter = \( 2 \cdot 3 + 6.0000 \approx 12.0000 \) feet.
Result: Perimeter = 12.0000 feet, Arc Length = 6.0000 feet.

5. Frequently Asked Questions (FAQ)

Q: What is a sector of a circle?
A: A sector is a portion of a circle bounded by two radii and the arc between them.

Q: Why use radians or degrees?
A: Radians provide a direct arc length calculation, while degrees are more intuitive for common angles.

Q: What if the angle exceeds 360° or 2π?
A: The calculator restricts angles to valid ranges (0° to 360° or 0 to 2π) for a single sector.