Perimeter of Rectangle with Given Area Calculator

Perimeter of Rectangle with Given Area Formula

1. What is the Perimeter of Rectangle with Given Area Calculator?

Definition: The Perimeter of Rectangle with Given Area Calculator computes the perimeter and the other side of a rectangle when the area and one side (length or width) are provided.

Purpose: Assists in calculating the boundary length and missing dimension of a rectangle for applications in design, construction, or education with customizable units.

2. How Does the Calculator Work?

The calculator uses the following relationships:

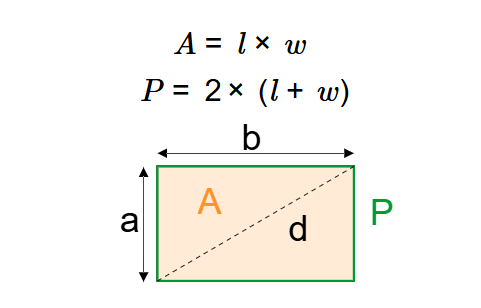
Area Formula:

\[ A = l \times w \]

Perimeter Formula:

\[ P = 2 \times (l + w) \]

Where:

\( A \): Area.
\( l \): Length.
\( w \): Width.
\( P \): Perimeter.

Steps:

Step 1: Input Area. Enter the area of the rectangle.
Step 2: Input Known Side. Provide the length or width.
Step 3: Select Unit. Choose from cm, m, inch, feet, or yard.
Step 4: Calculate. Compute the perimeter and the other side with fixed 4 decimal place precision.

3. Importance of Rectangle Perimeter Calculation with Given Area

Calculating the perimeter with a given area is crucial for:

Construction: Estimating boundary materials when area is fixed.
Design: Planning rectangular layouts with known space constraints.
Education: Teaching relationships between area, perimeter, and dimensions.

4. Using the Calculator

Example 1: Area 140 cm², Known Side 14 cm:

Step 1: Area = 140 cm².
Step 2: Known Side = 14 cm.
Step 3: Other Side = \( 140 / 14 = 10 \) cm.
Step 4: Perimeter = \( 2 \times (14 + 10) = 48 \) cm.
Result: Perimeter = 48.0000 cm, Other Side = 10.0000 cm.

Example 2: Area 15 inch², Known Side 3 inches:

Step 1: Area = 15 inch².
Step 2: Known Side = 3 inches.
Step 3: Other Side = \( 15 / 3 = 5 \) inches.
Step 4: Perimeter = \( 2 \times (3 + 5) = 16 \) inches.
Result: Perimeter = 16.0000 inches, Other Side = 5.0000 inches.

Example 3: Area 6 m², Known Side 2 m:

Step 1: Area = 6 m².
Step 2: Known Side = 2 m.
Step 3: Other Side = \( 6 / 2 = 3 \) m.
Step 4: Perimeter = \( 2 \times (2 + 3) = 10 \) m.
Result: Perimeter = 10.0000 m, Other Side = 3.0000 m.

Example 4: Area 12 feet², Known Side 3 feet:

Step 1: Area = 12 feet².
Step 2: Known Side = 3 feet.
Step 3: Other Side = \( 12 / 3 = 4 \) feet.
Step 4: Perimeter = \( 2 \times (3 + 4) = 14 \) feet.
Result: Perimeter = 14.0000 feet, Other Side = 4.0000 feet.

5. Frequently Asked Questions (FAQ)

Q: What is a rectangle?
A: A rectangle is a four-sided polygon with opposite sides equal and all angles 90°.

Q: Can I find the other side with this calculator?
A: Yes, it calculates the missing side (length or width) based on the area and known side.

Q: Why use unit conversion?
A: Unit conversion allows flexibility to match real-world measurements or preferences.