1. What is the Percent Agreement Calculator?

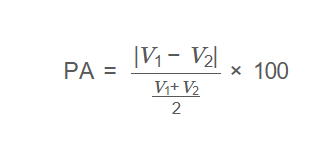
Definition: The Percent Agreement Calculator computes the percentage of agreement between two values, representing the relative difference between them as a percentage of their average. It quantifies how much two measurements or ratings differ.

Purpose: It is used in fields like psychology, sociology, and quality control to assess the consistency or discrepancy between two measurements, ratings, or observations, aiding in reliability analysis and process evaluation.

2. How Does the Calculator Work?

The calculator uses the following formula:

Formula: \[ \text{PA} = \frac{|V_1 - V_2|}{\frac{V_1 + V_2}{2}} \times 100 \] Where:

• \( \text{PA} \): Percent Agreement (%)
• \( V_1 \): First value
• \( V_2 \): Second value

Steps:

• Enter the first value (\( V_1 \)) and second value (\( V_2 \)).
• Calculate the absolute difference \( |V_1 - V_2| \).
• Compute the average \( \frac{V_1 + V_2}{2} \).
• Calculate \( \text{PA} \) by dividing the absolute difference by the average and multiplying by 100.
• Display the result with 4 decimal places.

3. Importance of Percent Agreement Calculation

Calculating percent agreement is crucial for:

• Reliability Analysis: Evaluates consistency between two raters or measurements in research or quality control.
• Decision-Making: Quantifies differences to support informed choices in collaborative settings.
• Scientific Studies: Assesses agreement in experiments, such as inter-rater reliability in psychology or sociology.
• Process Improvement: Identifies discrepancies to enhance measurement techniques or processes.

4. Using the Calculator

Example: Calculate the percent agreement for two measurements: \( V_1 = 25 \), \( V_2 = 20 \).

1. Enter \( V_1 = 25 \), \( V_2 = 20 \).
2. The calculator computes:
   • Average = \( \frac{25 + 20}{2} = 22.5 \)
   • Absolute difference = \( |25 - 20| = 5 \)
   • \( \text{PA} = \frac{5}{22.5} \times 100 \approx 22.2222 \)
3. The calculator returns:
   • \( \text{PA} \): 22.2222 %

Example: Calculate the percent agreement for two ratings: \( V_1 = 100 \), \( V_2 = 95 \).

1. Enter \( V_1 = 100 \), \( V_2 = 95 \).
2. The calculator computes:
   • Average = \( \frac{100 + 95}{2} = 97.5 \)
   • Absolute difference = \( |100 - 95| = 5 \)
   • \( \text{PA} = \frac{5}{97.5} \times 100 \approx 5.1282 \)
3. The calculator returns:
   • \( \text{PA} \): 5.1282 %

5. Frequently Asked Questions (FAQ)

Q: What is percent agreement?
A: Percent agreement (\( \text{PA} \)) measures the relative difference between two values as a percentage of their average, indicating how much they differ.

Q: How does this percent agreement formula differ from other definitions?
A: This formula measures the relative difference as a percentage. Other definitions, like inter-rater reliability, may count exact matches divided by total observations. This calculator uses the relative difference approach.

Q: Can percent agreement exceed 100%?
A: No, percent agreement is typically between 0% and 100%, though this formula can yield values above 100% for large differences (e.g., if \( |V_1 - V_2| > \frac{V_1 + V_2}{2} \)).

Q: What is a good percent agreement?
A: Lower values indicate less agreement (more difference). Context matters, but values below 10% suggest high similarity, while higher values indicate greater discrepancy.

Percent Agreement Calculator© - All Rights Reserved 2025