1. What is a Parallelogram Area Calculator?
Definition: This calculator computes the area of a parallelogram, a four-sided shape with opposite sides equal and parallel, based on three input scenarios: Base and Height, Sides + Angle Between, and Diagonals + Angle Between.
Purpose: It assists in geometry education, engineering, and design by calculating areas for applications like land measurement, flooring, and structural analysis.
2. How Does the Calculator Work?
The calculator supports three input scenarios for defining the parallelogram:
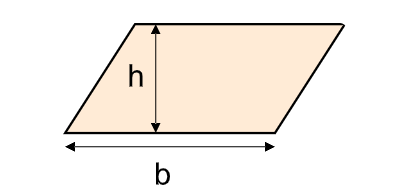
- Base and Height:
- Area: \( A = b \times h \).
- Sides + Angle Between:
- Area: \( A = a \times b \times \sin(\alpha) \).
- Diagonals + Angle Between:
- Area: \( A = \frac{1}{2} \times e \times f \times \sin(\theta) \), where \( \theta \) is the acute angle between diagonals.
Unit Conversions:
- Length Units: m, cm (1 m = 100 cm), mm (1 m = 1000 mm), in (1 m = 39.3701 in), ft (1 m = 3.28084 ft), yd (1 m = 1.09361 yd).
- Area Units: m², cm² (1 m² = 10000 cm²), mm² (1 m² = 1000000 mm²), in² (1 m² = 1550.0031 in²), ft² (1 m² = 10.7639 ft²), yd² (1 m² = 1.19599 yd²).
- Angle Units: Degrees.
Steps:
- Select the input scenario for the parallelogram.
- Input the required dimensions (base, height, sides, diagonals, angles) and select their units.
- Validate inputs (positive values, valid angles).
- Convert inputs to meters for calculations.
- Compute the area using the appropriate formula.
- Convert outputs to the selected units and format to 4 decimal places or scientific notation for small values.
3. Importance of Parallelogram Area Calculations
Calculating the area of parallelograms is crucial for:
- Geometry Education: Understanding properties of quadrilaterals.
- Architecture and Engineering: Designing structures with parallelogram-shaped components, such as beams or panels.
- Land Surveying: Measuring plots with parallelogram shapes.
4. Using the Calculator
Examples:
- Base and Height: Base \( b = 5 \, \text{cm} \), Height \( h = 3 \, \text{cm} \)
Convert: \( b = 0.05 \, \text{m} \), \( h = 0.03 \, \text{m} \).
Area: \( A = 0.05 \times 0.03 = 0.0015 \, \text{m}^2 = 15.0000 \, \text{cm}^2 \).
- Sides + Angle Between: Side \( a = 4 \, \text{cm} \), Side \( b = 6 \, \text{cm} \), Angle \( \alpha = 60^\circ \)
Convert: \( a = 0.04 \, \text{m} \), \( b = 0.06 \, \text{m} \).
Area: \( A = 0.04 \times 0.06 \times \sin(\pi/3) \approx 0.0021 \, \text{m}^2 = 20.7846 \, \text{cm}^2 \).
- Diagonals + Angle Between: Diagonal \( e = 8 \, \text{cm} \), Diagonal \( f = 10 \, \text{cm} \), Angle \( \theta = 45^\circ \)
Convert: \( e = 0.08 \, \text{m} \), \( f = 0.10 \, \text{m} \).
Area: \( A = \frac{1}{2} \times 0.08 \times 0.10 \times \sin(\pi/4) \approx 0.0028 \, \text{m}^2 = 28.2843 \, \text{cm}^2 \).
5. Frequently Asked Questions (FAQ)
Q: What is a parallelogram?
A: A parallelogram is a four-sided shape with opposite sides equal and parallel, including rectangles, rhombuses, and squares as special cases.
Q: Why does the diagonals scenario require an acute angle?
A: The area formula uses the acute angle between the diagonals to ensure the sine function yields a positive value, correctly reflecting the geometric configuration.
Q: Can the calculator handle special parallelograms like rectangles?
A: Yes, the calculator works for all parallelograms. For a rectangle, use Base and Height with a 90° angle in the Sides + Angle scenario, or ensure the angle between diagonals is 90°.
 Home
Home
 Back
Back