1. What is an Oblique Triangle Calculator?
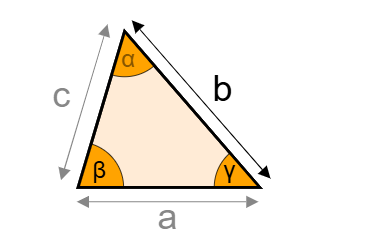
Definition: This calculator computes the properties of an oblique triangle, including angles, sides, and area, based on different input scenarios (SSS, SAS, ASA, AAS). An oblique triangle is any triangle without a right angle, including acute and obtuse triangles.
Purpose: It assists in geometry education, engineering, and design by solving triangles for applications like navigation, surveying, and structural analysis.
2. How Does the Calculator Work?
The calculator supports four input scenarios for defining the triangle:
- Three Sides (SSS):
- Angle \( \alpha \): \( \alpha = \cos^{-1}\left(\frac{b^2 + c^2 - a^2}{2bc}\right) \).
- Angle \( \beta \): \( \beta = \cos^{-1}\left(\frac{a^2 + c^2 - b^2}{2ac}\right) \).
- Angle \( \gamma \): \( \gamma = \cos^{-1}\left(\frac{a^2 + b^2 - c^2}{2ab}\right) \).
- Area: \( s = \frac{a + b + c}{2} \), \( A = \sqrt{s(s - a)(s - b)(s - c)} \).
- Two Sides + Angle Between (SAS):
- Side \( c \): \( c = \sqrt{a^2 + b^2 - 2ab \cos(\gamma)} \).
- Angle \( \alpha \): \( \alpha = \sin^{-1}\left(\frac{a \sin(\gamma)}{c}\right) \).
- Angle \( \beta \): \( \beta = 180^\circ - \alpha - \gamma \).
- Area: \( A = \frac{1}{2} a b \sin(\gamma) \).
- Two Angles + Side Between (ASA):
- Angle \( \gamma \): \( \gamma = 180^\circ - \alpha - \beta \).
- Side \( a \): \( a = c \frac{\sin(\alpha)}{\sin(\gamma)} \).
- Side \( b \): \( b = c \frac{\sin(\beta)}{\sin(\gamma)} \).
- Area: \( A = \frac{1}{2} a b \sin(\gamma) \).
- Two Angles + Adjacent Side (AAS):
- Angle \( \alpha \): \( \alpha = 180^\circ - \beta - \gamma \).
- Side \( a \): \( a = b \frac{\sin(\alpha)}{\sin(\beta)} \).
- Side \( c \): \( c = b \frac{\sin(\gamma)}{\sin(\beta)} \).
- Area: \( A = \frac{1}{2} a c \sin(\beta) \).
Unit Conversions:
- Length Units: m, cm (1 m = 100 cm), mm (1 m = 1000 mm), in (1 m = 39.3701 in), ft (1 m = 3.28084 ft), yd (1 m = 1.09361 yd).
- Area Units: m², cm² (1 m² = 10000 cm²), mm² (1 m² = 1000000 mm²), in² (1 m² = 1550.0031 in²), ft² (1 m² = 10.7639 ft²), yd² (1 m² = 1.19599 yd²).
- Angle Units: Degrees.
Steps:
- Select the input scenario for the triangle.
- Input the required dimensions (sides, angles) and select their units.
- Validate inputs (positive values, triangle inequalities, valid angles).
- Convert inputs to meters for calculations.
- Compute the angles, sides, and area using the appropriate formulas.
- Convert outputs to the selected units and format to 4 decimal places or scientific notation for small values.
3. Importance of Oblique Triangle Calculations
Calculating properties of oblique triangles is crucial for:
- Geometry Education: Understanding triangle properties and trigonometric laws.
- Surveying and Navigation: Determining distances and angles in land measurement or GPS systems.
- Engineering: Designing structures with triangular components, such as trusses.
4. Using the Calculator
Examples:
- Three Sides (SSS): Side \( a = 5 \, \text{cm} \), Side \( b = 6 \, \text{cm} \), Side \( c = 7 \, \text{cm} \)
Convert: \( a = 0.05 \, \text{m} \), \( b = 0.06 \, \text{m} \), \( c = 0.07 \, \text{m} \).
Angle \( \alpha \): \( \alpha = \cos^{-1}\left(\frac{0.06^2 + 0.07^2 - 0.05^2}{2 \times 0.06 \times 0.07}\right) \approx 41.4096^\circ \).
Angle \( \beta \): \( \beta = \cos^{-1}\left(\frac{0.05^2 + 0.07^2 - 0.06^2}{2 \times 0.05 \times 0.07}\right) \approx 55.7717^\circ \).
Angle \( \gamma \): \( \gamma = \cos^{-1}\left(\frac{0.05^2 + 0.06^2 - 0.07^2}{2 \times 0.05 \times 0.06}\right) \approx 82.8187^\circ \).
Area: \( s = \frac{0.05 + 0.06 + 0.07}{2} = 0.09 \), \( A = \sqrt{0.09 \times (0.09 - 0.05) \times (0.09 - 0.06) \times (0.09 - 0.07)} \approx 0.0015 \, \text{m}^2 = 14.6969 \, \text{cm}^2 \).
- Two Sides + Angle Between (SAS): Side \( a = 4 \, \text{cm} \), Angle \( \gamma = 45^\circ \), Side \( b = 5 \, \text{cm} \)
Convert: \( a = 0.04 \, \text{m} \), \( b = 0.05 \, \text{m} \).
Side \( c \): \( c = \sqrt{0.04^2 + 0.05^2 - 2 \times 0.04 \times 0.05 \times \cos(\pi/4)} \approx 0.0357 \, \text{m} = 3.5679 \, \text{cm} \).
Angle \( \alpha \): \( \alpha = \sin^{-1}\left(\frac{0.04 \times \sin(\pi/4)}{0.0357}\right) \approx 53.6596^\circ \).
Angle \( \beta \): \( \beta = 180 - 53.6596 - 45 \approx 81.3404^\circ \).
Area: \( A = \frac{1}{2} \times 0.04 \times 0.05 \times \sin(\pi/4) \approx 0.0007 \, \text{m}^2 = 7.0711 \, \text{cm}^2 \).
- Two Angles + Side Between (ASA): Angle \( \alpha = 30^\circ \), Side \( c = 10 \, \text{cm} \), Angle \( \beta = 60^\circ \)
Convert: \( c = 0.1 \, \text{m} \).
Angle \( \gamma \): \( \gamma = 180 - 30 - 60 = 90^\circ \).
Side \( a \): \( a = 0.1 \times \frac{\sin(\pi/6)}{\sin(\pi/2)} \approx 0.05 \, \text{m} = 5.0000 \, \text{cm} \).
Side \( b \): \( b = 0.1 \times \frac{\sin(\pi/3)}{\sin(\pi/2)} \approx 0.0866 \, \text{m} = 8.6603 \, \text{cm} \).
Area: \( A = \frac{1}{2} \times 0.05 \times 0.0866 \times \sin(\pi/2) \approx 0.0022 \, \text{m}^2 = 21.6506 \, \text{cm}^2 \).
- Two Angles + Adjacent Side (AAS): Angle \( \beta = 40^\circ \), Angle \( \gamma = 50^\circ \), Side \( b = 8 \, \text{cm} \)
Convert: \( b = 0.08 \, \text{m} \).
Angle \( \alpha \): \( \alpha = 180 - 40 - 50 = 90^\circ \).
Side \( a \): \( a = 0.08 \times \frac{\sin(\pi/2)}{\sin(2\pi/9)} \approx 0.1247 \, \text{m} = 12.4672 \, \text{cm} \).
Side \( c \): \( c = 0.08 \times \frac{\sin(5\pi/18)}{\sin(2\pi/9)} \approx 0.0958 \, \text{m} = 9.5820 \, \text{cm} \).
Area: \( A = \frac{1}{2} \times 0.1247 \times 0.0958 \times \sin(2\pi/9) \approx 0.0046 \, \text{m}^2 = 45.9556 \, \text{cm}^2 \).
5. Frequently Asked Questions (FAQ)
Q: What is an oblique triangle?
A: An oblique triangle is any triangle that does not have a right angle, including acute (all angles less than 90°) and obtuse (one angle greater than 90°) triangles.
Q: How is the area calculated for different scenarios?
A: The area is calculated using Heron's formula for SSS (based on side lengths) or the formula \( A = \frac{1}{2} \times \text{side}_1 \times \text{side}_2 \times \sin(\text{angle}) \) for SAS, ASA, and AAS, using the appropriate sides and angle.
Q: Why does the SSS scenario use the Law of Cosines?
A: The Law of Cosines is used to find angles when all three sides are known, as it relates the sides to the cosine of the opposite angle, allowing angle calculation.
 Home
Home
 Back
Back