Negative Log Calculator

1. What is a Negative Log Calculator?

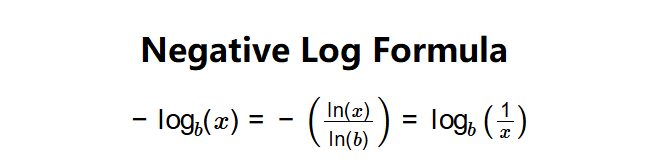
Definition: This calculator computes the negative logarithm of a number \( x \) with respect to a specified base \( b \), i.e., \( -\log_b(x) \), which is the negative of the exponent \( y \) such that \( b^y = x \). It can also be interpreted as the logarithm of the reciprocal: \( \log_b\left(\frac{1}{x}\right) \).

Purpose: It aids in scientific fields like chemistry (e.g., calculating pH), signal processing, and engineering by transforming logarithmic values, often to express small probabilities or concentrations in a more manageable form.

2. How Does the Calculator Work?

The calculator uses the following logarithmic relationship:

Negative Logarithm: \( -\log_b(x) = -\left(\frac{\ln(x)}{\ln(b)}\right) = \log_b\left(\frac{1}{x}\right) \)

Steps:

Input the number \( x \) (positive) and the base \( b \) (positive, not 1).
Validate inputs (\( x > 0 \), \( b > 0 \), \( b \neq 1 \)).
Compute the logarithm \( \log_b(x) = \frac{\ln(x)}{\ln(b)} \).
Calculate the negative logarithm by negating the result: \( -\log_b(x) \).
Format the output to 4 decimal places or scientific notation for very small or large values.

3. Importance of Negative Log Calculations

Negative logarithm calculations are essential for:

Chemistry: Determining the pH of a solution, where \( \text{pH} = -\log_{10}([H^+]) \), and \( [H^+] \) is the hydrogen ion concentration.
Signal Processing: Measuring signal-to-noise ratios, often expressed as \( -10 \log_{10}(\text{ratio}) \).
Mathematics: Simplifying expressions involving small probabilities or concentrations, such as in statistical mechanics or information theory.

4. Using the Calculator

Examples:

pH Calculation: Number \( x = 0.001 \), Base \( b = 10 \)
\( -\log_{10}(0.001) = -(-3) = 3.0000 \), which corresponds to a pH of 3 for a solution with \( [H^+] = 0.001 \).
Binary Negative Log: Number \( x = 8 \), Base \( b = 2 \)
\( -\log_2(8) = -(3) = -3.0000 \), since \( 2^3 = 8 \).
Natural Negative Log: Number \( x = 2.7183 \), Base \( b = e \approx 2.7183 \)
\( -\ln(2.7183) \approx -(1) = -1.0000 \), since \( \ln(e) = 1 \).

5. Frequently Asked Questions (FAQ)

Q: What is a negative logarithm?
A: A negative logarithm \( -\log_b(x) \) is the negative of the logarithm, equivalent to \( \log_b\left(\frac{1}{x}\right) \). It represents how many times 1 must be divided by the base to obtain the number \( x \).

Q: Why must the number \( x \) be positive?
A: In the real number system, logarithms are defined only for positive arguments, as there is no real number \( y \) such that \( b^y \leq 0 \) for \( b > 0 \).

Q: How is the negative logarithm used in chemistry?
A: It’s used to calculate pH, a measure of acidity, where \( \text{pH} = -\log_{10}([H^+]) \). For example, a hydrogen ion concentration of \( 10^{-7} \) M yields a pH of 7.