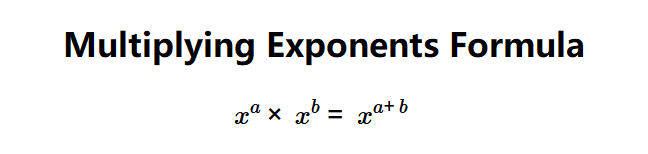Multiplying Exponents Calculator

1. What is a Multiplying Exponents Calculator?

Definition: This calculator computes the product of two exponential expressions, \( x^a \times y^b \), given the bases \( x \) and \( y \), and exponents \( a \) and \( b \). It handles cases where the bases are the same or different, applying exponent rules where applicable.

Purpose: It aids in mathematics education, algebra, and scientific calculations by simplifying the multiplication of exponential expressions, useful in fields like physics, engineering, and finance.

2. How Does the Calculator Work?

The calculator uses the following exponent rules:

Same Bases: \( x^a \times x^b = x^{a+b} \)
Different Bases: \( x^a \times y^b = (x^a) \times (y^b) \) (computed numerically)
Negative Exponent: \( x^{-a} = \frac{1}{x^a} \)
Zero Exponent: \( x^0 = 1 \)

Steps:

Input the bases \( x \) and \( y \), and exponents \( a \) and \( b \).
Validate inputs (\( x \neq 0 \), \( y \neq 0 \) when exponents are non-zero).
If bases are the same, apply the product rule: \( x^{a+b} \).
If bases are different, compute \( x^a \) and \( y^b \), then multiply: \( (x^a) \times (y^b) \).
Handle special cases: negative exponents as fractions, zero exponents as 1.
Format the output to 4 decimal places or scientific notation for very small or large values.

3. Importance of Multiplying Exponents

Multiplying exponents is essential for:

Mathematics Education: Understanding exponent rules and simplifying expressions.
Science and Engineering: Simplifying calculations in exponential growth, decay, or scaling laws.
Data Analysis: Handling exponential data in fields like finance (compound interest) or biology (population growth).

4. Using the Calculator

Examples:

Same Bases: Base \( x = 5 \), Exponent \( a = 2 \), Base \( y = 5 \), Exponent \( b = 3 \)
Since bases are the same, \( 5^2 \times 5^3 = 5^{2+3} = 5^5 = 3125.0000 \).
Different Bases: Base \( x = 2 \), Exponent \( a = 3 \), Base \( y = 3 \), Exponent \( b = 2 \)
Compute separately: \( 2^3 = 8 \), \( 3^2 = 9 \), then \( 8 \times 9 = 72.0000 \).
Negative Exponent: Base \( x = 4 \), Exponent \( a = -2 \), Base \( y = 3 \), Exponent \( b = 1 \)
Compute: \( 4^{-2} = \frac{1}{4^2} = \frac{1}{16} = 0.0625 \), \( 3^1 = 3 \), then \( 0.0625 \times 3 = 0.1875 \).

5. Frequently Asked Questions (FAQ)

Q: What does multiplying exponents mean?
A: Multiplying exponents means finding the product of two exponential terms, \( x^a \times y^b \), either by adding exponents (same bases) or computing numerically (different bases).

Q: What happens if the bases are the same?
A: If the bases are the same, add the exponents: \( x^a \times x^b = x^{a+b} \).

Q: How are negative exponents handled?
A: A negative exponent indicates a reciprocal: \( x^{-a} = \frac{1}{x^a} \), which is computed before multiplying.