Log Base 2 Calculator

1. What is a Log Base 2 Calculator?

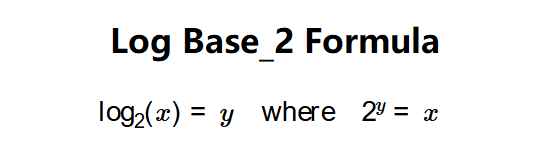
Definition: This calculator computes the logarithm base 2 of a number \( x \), i.e., \( \log_2(x) \), which is the exponent \( y \) such that \( 2^y = x \). Also known as the binary logarithm, it is particularly useful in fields like computer science and information theory.

Purpose: It aids in solving problems involving binary systems, such as computing the number of bits needed to represent data, analyzing algorithm complexity, or calculating entropy in information theory.

2. How Does the Calculator Work?

The calculator uses the following logarithmic relationship:

Binary Logarithm: \( \log_2(x) = y \quad \text{where} \quad 2^y = x \)

Steps:

Input the logarithm argument \( x \) (positive).
Validate the input (\( x > 0 \)).
Compute the binary logarithm using \( \log_2(x) = \frac{\ln(x)}{\ln(2)} \).
Format the output to 4 decimal places or scientific notation for very small or large values.

3. Importance of Log Base 2 Calculations

Binary logarithm calculations are essential for:

Computer Science: Determining the number of bits required to represent data or analyzing the time complexity of algorithms (e.g., binary search).
Information Theory: Calculating entropy or information content in bits, which is fundamental for data compression and cryptography.
Mathematics Education: Understanding the inverse relationship between logarithms and exponentials, especially in base 2.

4. Using the Calculator

Examples:

Power of 2: Logarithm of \( x = 8 \)
Result: \( \log_2(8) = 3.0000 \), since \( 2^3 = 8 \).
Non-Power of 2: Logarithm of \( x = 10 \)
Result: \( \log_2(10) \approx 3.3219 \), since \( 2^{3.3219} \approx 10 \).
Small Number: Logarithm of \( x = 0.5 \)
Result: \( \log_2(0.5) = -1.0000 \), since \( 2^{-1} = 0.5 \).

5. Frequently Asked Questions (FAQ)

Q: What is a binary logarithm?
A: A binary logarithm \( \log_2(x) \) is the exponent \( y \) such that \( 2^y = x \). It’s called binary because the base is 2, aligning with binary systems used in computing.

Q: Why must the argument be positive?
A: In the real number system, logarithms are defined only for positive arguments, as there is no real number \( y \) such that \( 2^y \leq 0 \).

Q: How is the binary logarithm used in computing?
A: It’s used to calculate the number of bits needed to represent data (e.g., \( \log_2(16) = 4 \) bits for 16 values) or to analyze the efficiency of algorithms like binary search, which has a time complexity of \( \log_2(n) \).