Kite Area Calculator - Find Area and Perimeter

Calculation Method:

Diagonal \( e \):

Diagonal \( f \):

Side \( a \):

Side \( b \):

Angle \( \alpha \) (between \( a \) and \( b \)):

1. What is a Kite Area Calculator?

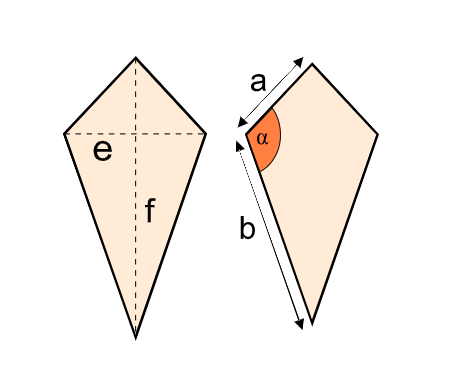
Definition: This calculator computes the area of a kite using either the lengths of its two diagonals (\( e \) and \( f \)) or the lengths of two unequal sides (\( a \) and \( b \)) and the angle between them (\( \alpha \)). For the sides and angle method, it also calculates the perimeter. A kite is a quadrilateral with two pairs of adjacent sides equal.

Purpose: It aids in geometry education, architectural design, and engineering by providing area and perimeter measurements for kite-shaped objects, such as sails, kites, or structural panels.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Diagonals Method:
- Area: \( \text{Area} = \frac{1}{2} \cdot e \cdot f \).
Sides and Angle Method:
- Area: \( \text{Area} = a \cdot b \cdot \sin(\alpha) \).
- Perimeter: \( \text{Perimeter} = 2 \cdot (a + b) \).

Unit Conversions:

Length Units: m, cm (1 m = 100 cm), mm (1 m = 1000 mm), in (1 m = 39.3701 in), ft (1 m = 3.28084 ft), yd (1 m = 1.09361 yd).
Area Units: m², cm² (1 m² = 10000 cm²), mm² (1 m² = 1000000 mm²), in² (1 m² = 1550.0031 in²), ft² (1 m² = 10.7639 ft²), yd² (1 m² = 1.19599 yd²).
Angle Units: Angles are input and computed in degrees.

Steps:

Select the calculation method (diagonals or sides and angle).
For diagonals: Input the lengths of diagonals \( e \) and \( f \), selecting their units.
For sides and angle: Input the lengths of sides \( a \) and \( b \), their units, and the angle \( \alpha \) in degrees.
Validate inputs: Diagonals and sides must be positive; angle must be between 0° and 180°.
Convert inputs to meters for calculations.
Compute the area (and perimeter for sides and angle method) using the formulas above.
Convert outputs to the selected units.
Format outputs to 4 decimal places or scientific notation for small values.

3. Importance of Kite Area Calculations

Calculating the area and perimeter of a kite is crucial for:

Geometry Education: Understanding quadrilateral properties and trigonometric applications.
Design and Manufacturing: Determining material requirements for kite-shaped objects, such as sails, parachutes, or decorative panels.
Engineering: Analyzing structural components with kite-like shapes in architecture or aerospace.

4. Using the Calculator

Examples:

Example 1 (Diagonals): Diagonal \( e = 4 \, \text{cm} \), Diagonal \( f = 6 \, \text{cm} \)
- Convert: \( e = 0.04 \, \text{m} \), \( f = 0.06 \, \text{m} \).
- Area: \( \text{Area} = \frac{1}{2} \cdot 0.04 \cdot 0.06 = 0.0012 \, \text{m}^2 = 12.0000 \, \text{cm}^2 \).
Example 2 (Sides and Angle): Side \( a = 2 \, \text{m} \), Side \( b = 3 \, \text{m} \), Angle \( \alpha = 60^\circ \)
- Area: \( \text{Area} = 2 \cdot 3 \cdot \sin(60^\circ) \approx 2 \cdot 3 \cdot 0.8660 = 5.1962 \, \text{m}^2 \).
- Perimeter: \( \text{Perimeter} = 2 \cdot (2 + 3) = 10.0000 \, \text{m} \).

5. Frequently Asked Questions (FAQ)

Q: What is a kite?
A: A kite is a quadrilateral with two pairs of adjacent sides equal, often resembling the shape of a traditional kite with diagonals that intersect at right angles.

Q: Why do the diagonals method and sides method give different inputs?
A: The diagonals method uses the kite’s symmetry and perpendicular diagonals to calculate area directly, while the sides and angle method uses trigonometric properties of the triangle formed by two sides, requiring the angle between them.

Q: Can the calculator handle any kite shape?
A: Yes, as long as the inputs describe a valid kite (positive diagonals or sides, and an angle between 0° and 180°), the calculator provides accurate results.