Isosceles Triangle Side Calculator - Find Base Angle, Area, Perimeter, Leg, Base

Base angle \( \alpha \):

Area:

Perimeter:

Leg \( a \):

Base \( b \):

1. What is an Isosceles Triangle Side Calculator?

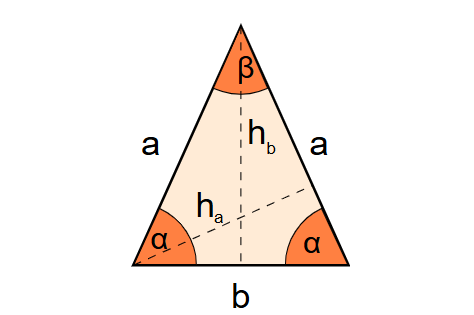
Definition: This calculator computes the base angle (\( \alpha \)), area, perimeter, leg length (\( a \)), and base length (\( b \)) of an isosceles triangle, given the vertex angle (\( \beta \)) and the height from the apex (\( h_b \)). An isosceles triangle is a three-sided polygon with two sides of equal length (legs) and two equal base angles.

Purpose: It assists in geometry education, architectural design, and engineering by providing key measurements for isosceles triangles, useful for structural calculations, area computations, and design planning.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Base angle \( \alpha \): \( \alpha = \frac{180^\circ - \beta}{2} \).
Leg length \( a \): \( a = \frac{h_b}{\sin(\alpha)} \).
Base length \( b \): \( b = 2 \cdot a \cdot \cos(\alpha) \).
Area: \( \text{Area} = \frac{1}{2} \cdot b \cdot h_b \).
Perimeter: \( \text{Perimeter} = 2a + b \).

Unit Conversions:

Length Units: m, cm (1 m = 100 cm), mm (1 m = 1000 mm), in (1 m = 39.3701 in), ft (1 m = 3.28084 ft), yd (1 m = 1.09361 yd).
Area Units: m², cm² (1 m² = 10000 cm²), mm² (1 m² = 1000000 mm²), in² (1 m² = 1550.0031 in²), ft² (1 m² = 10.7639 ft²), yd² (1 m² = 1.19599 yd²).
Angle Units: Angles are computed and displayed in degrees.

Steps:

Input the vertex angle \( \beta \) in degrees and the height from the apex \( h_b \), selecting its unit.
Validate inputs: \( \beta \) must be between 0° and 180°, and \( h_b \) must be positive.
Convert the height to meters for calculations.
Compute the base angle, leg length, base length, area, and perimeter using the formulas above.
Convert outputs to the selected units.
Format outputs to 4 decimal places or scientific notation for small values.

3. Importance of Isosceles Triangle Side Calculations

Calculating the properties of an isosceles triangle is crucial for:

Geometry Education: Understanding triangle properties and trigonometric relationships.
Architecture and Design: Determining dimensions for structural or aesthetic elements, such as roof pitches or triangular supports.
Engineering: Analyzing forces, areas, or material requirements in structures with isosceles triangular components.

4. Using the Calculator

Examples:

Example 1: Vertex angle \( \beta = 60^\circ \), Height \( h_b = 2 \, \text{cm} \)
- Convert: \( h_b = 0.02 \, \text{m} \).
- Base angle: \( \alpha = \frac{180 - 60}{2} = 60^\circ \).
- Leg length: \( a = \frac{0.02}{\sin(60^\circ)} \approx 0.0231 \, \text{m} = 2.3094 \, \text{cm} \).
- Base length: \( b = 2 \cdot 0.0231 \cdot \cos(60^\circ) \approx 0.0231 \, \text{m} = 2.3094 \, \text{cm} \).
- Area: \( \text{Area} = \frac{1}{2} \cdot 0.0231 \cdot 0.02 \approx 0.000231 \, \text{m}^2 = 2.3094 \, \text{cm}^2 \).
- Perimeter: \( \text{Perimeter} = 2 \cdot 0.0231 + 0.0231 \approx 0.0693 \, \text{m} = 6.9282 \, \text{cm} \).
Example 2: Vertex angle \( \beta = 40^\circ \), Height \( h_b = 1 \, \text{m} \)
- Base angle: \( \alpha = \frac{180 - 40}{2} = 70^\circ \).
- Leg length: \( a = \frac{1}{\sin(70^\circ)} \approx 1.0642 \, \text{m} \).
- Base length: \( b = 2 \cdot 1.0642 \cdot \cos(70^\circ) \approx 0.7280 \, \text{m} \).
- Area: \( \text{Area} = \frac{1}{2} \cdot 0.7280 \cdot 1 \approx 0.3640 \, \text{m}^2 \).
- Perimeter: \( \text{Perimeter} = 2 \cdot 1.0642 + 0.7280 \approx 2.8564 \, \text{m} \).

5. Frequently Asked Questions (FAQ)

Q: What is an isosceles triangle?
A: An isosceles triangle is a triangle with two sides of equal length (legs) and two equal base angles opposite those sides.

Q: Why are the base angles equal?
A: The base angles are equal because they are opposite the two equal sides, as per the isosceles triangle theorem.

Q: How is the area of an isosceles triangle calculated?
A: The area is calculated as \( \text{Area} = \frac{1}{2} \cdot b \cdot h_b \), where \( b \) is the base length and \( h_b \) is the height from the apex to the base.