Isosceles Triangle Height Calculator - Find Height to Apex and Height from Leg

Height to apex \( h_b \):

Height from leg \( h_a \):

1. What is an Isosceles Triangle Height Calculator?

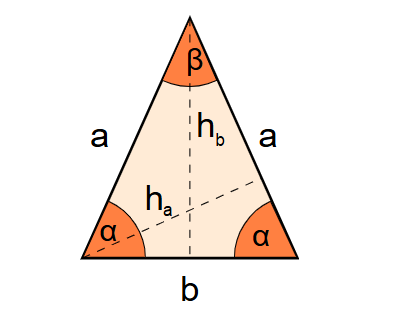
Definition: This calculator computes the heights of an isosceles triangle, specifically the height to the apex (\( h_b \)) from the base to the vertex and the height from the leg (\( h_a \)) derived from the apex height, given the lengths of the legs (\( a \)) and the base (\( b \)). An isosceles triangle is a three-sided polygon with two sides of equal length (legs).

Purpose: It aids in geometry education, architectural design, and engineering by providing height measurements for isosceles triangles, useful for calculating areas, structural supports, or design proportions.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Height to apex \( h_b \): Using the Pythagorean theorem in the right triangle formed by the height, half the base, and a leg: \( h_b = \sqrt{a^2 - \left(\frac{b}{2}\right)^2} \).
Height from leg \( h_a \): Derived from the height to the apex scaled by the base-to-leg ratio: \( h_a = h_b \cdot \frac{b}{a} \).

Unit Conversions:

Length Units: m, cm (1 m = 100 cm), mm (1 m = 1000 mm), in (1 m = 39.3701 in), ft (1 m = 3.28084 ft), yd (1 m = 1.09361 yd).

Steps:

Input the leg length \( a \) and base length \( b \), selecting their units.
Validate inputs: both must be positive, and \( b < 2a \) to form a valid triangle.
Convert inputs to meters for calculations.
Compute the height to the apex \( h_b \) using the Pythagorean theorem.
Calculate the height from the leg \( h_a \) using the formula \( h_a = h_b \cdot \frac{b}{a} \).
Convert outputs to the selected unit.
Format outputs to 4 decimal places or scientific notation for small values.

3. Importance of Isosceles Triangle Height Calculations

Calculating the heights of an isosceles triangle is crucial for:

Geometry Education: Understanding triangle properties and the Pythagorean theorem.
Architecture and Design: Determining heights for structural elements like triangular supports or roof trusses.
Engineering: Calculating areas or designing components with isosceles triangular shapes.

4. Using the Calculator

Examples:

Example 1: Leg \( a = 5 \, \text{cm} \), Base \( b = 6 \, \text{cm} \)
- Convert: \( a = 0.05 \, \text{m} \), \( b = 0.06 \, \text{m} \).
- Height to apex: \( h_b = \sqrt{0.05^2 - \left(\frac{0.06}{2}\right)^2} = \sqrt{0.0025 - 0.0009} \approx 0.04 \, \text{m} = 4.0000 \, \text{cm} \).
- Height from leg: \( h_a = 0.04 \cdot \frac{0.06}{0.05} = 0.048 \, \text{m} = 4.8000 \, \text{cm} \).
Example 2: Leg \( a = 2 \, \text{m} \), Base \( b = 3 \, \text{m} \)
- Height to apex: \( h_b = \sqrt{2^2 - \left(\frac{3}{2}\right)^2} = \sqrt{4 - 2.25} \approx 1.3229 \, \text{m} \).
- Height from leg: \( h_a = 1.3229 \cdot \frac{3}{2} \approx 1.9843 \, \text{m} \).

5. Frequently Asked Questions (FAQ)

Q: What is an isosceles triangle?
A: An isosceles triangle is a triangle with two sides of equal length (legs) and two equal angles opposite those sides.

Q: Why is the height to the apex important?
A: The height to the apex is used to calculate the triangle’s area (\( \text{Area} = \frac{1}{2} \cdot b \cdot h_b \)) and is critical for structural and design applications.

Q: What does the height from the leg represent?
A: The height from the leg (\( h_a \)) is derived from the height to the apex scaled by the base-to-leg ratio (\( h_a = h_b \cdot \frac{b}{a} \)), useful in specific geometric or engineering analyses.