1. What is the Isosceles Right Triangle Calculator?
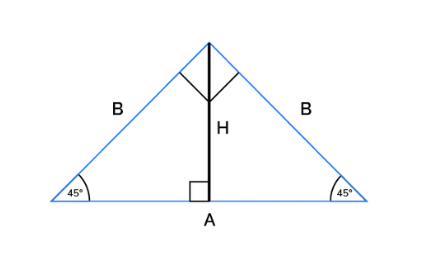
Definition: The Isosceles Right Triangle Calculator computes the hypotenuse, area, perimeter, and height of an isosceles right triangle, which has two equal legs and angles of 45°, 45°, and 90°.
Purpose: Assists in calculating geometric properties for isosceles right triangles used in construction, design, or education with customizable units.
2. How Does the Calculator Work?
The calculator uses the following formulas:
Hypotenuse:
\[ h = l \cdot \sqrt{2} \]
Area:
\[ A = \frac{1}{2} \cdot l \cdot l = \frac{l^2}{2} \]
Perimeter:
\[ P = 2 \cdot l + h = 2 \cdot l + l \cdot \sqrt{2} \]
Height (to Hypotenuse):
\[ H = \frac{l}{\sqrt{2}} \]
Where:
- \( l \): Length of each leg (equal sides).
- \( h \): Hypotenuse.
- \( A \): Area.
- \( P \): Perimeter.
- \( H \): Height from the right angle to the hypotenuse.
Steps:
- Step 1: Input Leg Length. Enter a positive value for the length of one leg.
- Step 2: Select Unit. Choose from cm, m, inch, feet, or yard.
- Step 3: Calculate. Compute the hypotenuse, area, perimeter, and height with fixed 4 decimal place precision.
3. Importance of Isosceles Right Triangle Calculation
Calculating isosceles right triangle properties is crucial for:
- Construction: Designing right-angled structures with equal legs.
- Design: Creating symmetrical patterns or frameworks.
- Education: Teaching special right triangle properties and the Pythagorean theorem.
4. Using the Calculator
Example 1: Leg Length 5 cm:
- Step 1: Leg Length = 5 cm.
- Step 2: Hypotenuse = \( 5 \cdot \sqrt{2} \approx 7.0711 \) cm.
- Step 3: Area = \( \frac{5^2}{2} = 12.5000 \) square cm.
- Step 4: Perimeter = \( 2 \cdot 5 + 7.0711 \approx 17.0711 \) cm.
- Step 5: Height = \( \frac{5}{\sqrt{2}} \approx 3.5355 \) cm.
- Result: Hypotenuse ≈ 7.0711 cm, Area = 12.5000 square cm, Perimeter ≈ 17.0711 cm, Height ≈ 3.5355 cm.
Example 2: Leg Length 3 inches:
- Step 1: Leg Length = 3 inches.
- Step 2: Hypotenuse = \( 3 \cdot \sqrt{2} \approx 4.2426 \) inches.
- Step 3: Area = \( \frac{3^2}{2} = 4.5000 \) square inches.
- Step 4: Perimeter = \( 2 \cdot 3 + 4.2426 \approx 10.2426 \) inches.
- Step 5: Height = \( \frac{3}{\sqrt{2}} \approx 2.1213 \) inches.
- Result: Hypotenuse ≈ 4.2426 inches, Area = 4.5000 square inches, Perimeter ≈ 10.2426 inches, Height ≈ 2.1213 inches.
Example 3: Leg Length 2 m:
- Step 1: Leg Length = 2 m.
- Step 2: Hypotenuse = \( 2 \cdot \sqrt{2} \approx 2.8284 \) m.
- Step 3: Area = \( \frac{2^2}{2} = 2.0000 \) square m.
- Step 4: Perimeter = \( 2 \cdot 2 + 2.8284 \approx 6.8284 \) m.
- Step 5: Height = \( \frac{2}{\sqrt{2}} \approx 1.4142 \) m.
- Result: Hypotenuse ≈ 2.8284 m, Area = 2.0000 square m, Perimeter ≈ 6.8284 m, Height ≈ 1.4142 m.
Example 4: Leg Length 4 feet:
- Step 1: Leg Length = 4 feet.
- Step 2: Hypotenuse = \( 4 \cdot \sqrt{2} \approx 5.6569 \) feet.
- Step 3: Area = \( \frac{4^2}{2} = 8.0000 \) square feet.
- Step 4: Perimeter = \( 2 \cdot 4 + 5.6569 \approx 13.6569 \) feet.
- Step 5: Height = \( \frac{4}{\sqrt{2}} \approx 2.8284 \) feet.
- Result: Hypotenuse ≈ 5.6569 feet, Area = 8.0000 square feet, Perimeter ≈ 13.6569 feet, Height ≈ 2.8284 feet.
5. Frequently Asked Questions (FAQ)
Q: What is an isosceles right triangle?
A: An isosceles right triangle is a right-angled triangle with two equal legs and angles of 45°, 45°, and 90°.
Q: How is the height calculated?
A: The height from the right angle to the hypotenuse is \( \frac{l}{\sqrt{2}} \), derived from the triangle's symmetry.
Q: Can the calculator handle other units?
A: Yes, it supports cm, m, inch, feet, and yard with automatic conversion.
Isosceles Right Triangle Calculator© - All Rights Reserved 2025
 Home
Home
 Back
Back