Hollow Cylinder Calculator - Find Thickness and Volume

Height \( h \):

Outer diameter \( D \):

Inner diameter \( d \):

Thickness:

Volume:

1. What is a Hollow Cylinder Calculator?

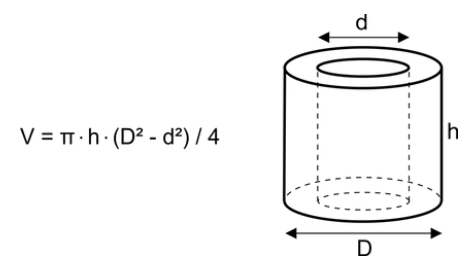
Definition: This calculator computes the thickness and volume of a hollow cylinder, given the height (\( h \)), outer diameter (\( D \)), and inner diameter (\( d \)). A hollow cylinder is a three-dimensional shape with two concentric circular bases connected by curved surfaces, forming a tube-like structure.

Purpose: It aids in engineering, manufacturing, and design by providing measurements for hollow cylindrical objects, such as pipes, tubes, or containers, useful for calculating material volume or capacity.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Outer radius \( R \): \( R = \frac{D}{2} \).
Inner radius \( r \): \( r = \frac{d}{2} \).
Thickness \( t \): \( t = R - r = \frac{D - d}{2} \).
Volume \( V \): \( V = \pi \cdot h \cdot (R^2 - r^2) = \pi \cdot h \cdot \left( \left(\frac{D}{2}\right)^2 - \left(\frac{d}{2}\right)^2 \right) \).

Unit Conversions:

Length Units: m, cm (1 m = 100 cm), mm (1 m = 1000 mm), in (1 m = 39.3701 in), ft (1 m = 3.28084 ft), yd (1 m = 1.09361 yd).
Volume Units: m³, cm³ (1 m³ = 1000000 cm³), mm³ (1 m³ = 1000000000 mm³), in³ (1 m³ = 61023.7441 in³), ft³ (1 m³ = 35.3147 ft³), yd³ (1 m³ = 1.30795 yd³).

Steps:

Input the height \( h \), outer diameter \( D \), and inner diameter \( d \), selecting their units.
Validate inputs: All must be positive; \( d < D \).
Convert inputs to meters for calculations.
Compute the thickness and volume using the formulas above.
Convert outputs to the selected units.
Format outputs to 4 decimal places or scientific notation for small values.

3. Importance of Hollow Cylinder Calculations

Calculating the properties of a hollow cylinder is crucial for:

Engineering: Designing pipes, tubes, or pressure vessels with precise material requirements.
Manufacturing: Determining the volume of material needed or the capacity of cylindrical containers.
Construction: Analyzing structural components like columns or conduits.

4. Using the Calculator

Examples:

Example 1: Height \( h = 20 \, \text{cm} \), Outer diameter \( D = 10 \, \text{cm} \), Inner diameter \( d = 8 \, \text{cm} \)
- Convert: \( h = 0.2 \, \text{m} \), \( D = 0.1 \, \text{m} \), \( d = 0.08 \, \text{m} \).
- Outer radius: \( R = \frac{0.1}{2} = 0.05 \, \text{m} \).
- Inner radius: \( r = \frac{0.08}{2} = 0.04 \, \text{m} \).
- Thickness: \( t = 0.05 - 0.04 = 0.01 \, \text{m} = 1.0000 \, \text{cm} \).
- Volume: \( V = \pi \cdot 0.2 \cdot (0.05^2 - 0.04^2) = \pi \cdot 0.2 \cdot (0.0025 - 0.0016) \approx 0.0005655 \, \text{m}^3 = 565.4867 \, \text{cm}^3 \).
Example 2: Height \( h = 1 \, \text{m} \), Outer diameter \( D = 0.5 \, \text{m} \), Inner diameter \( d = 0.4 \, \text{m} \)
- Outer radius: \( R = \frac{0.5}{2} = 0.25 \, \text{m} \).
- Inner radius: \( r = \frac{0.4}{2} = 0.2 \, \text{m} \).
- Thickness: \( t = 0.25 - 0.2 = 0.05 \, \text{m} \).
- Volume: \( V = \pi \cdot 1 \cdot (0.25^2 - 0.2^2) = \pi \cdot 1 \cdot (0.0625 - 0.04) \approx 0.0707 \, \text{m}^3 \).

5. Frequently Asked Questions (FAQ)

Q: What is a hollow cylinder?
A: A hollow cylinder is a three-dimensional shape with two concentric circular bases connected by curved surfaces, forming a tube with an outer diameter \( D \), inner diameter \( d \), and height \( h \).

Q: Why is the thickness important?
A: The thickness represents the wall thickness of the cylinder, critical for determining material strength, weight, and structural integrity in applications like piping or tubing.

Q: How is the volume of a hollow cylinder derived?
A: The volume is the difference between the volumes of two solid cylinders with radii \( R \) and \( r \), calculated as \( V = \pi \cdot h \cdot (R^2 - r^2) \).