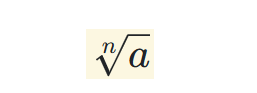Fifth Root Calculator - Find the Fifth Root of a Number

1. What is a Fifth Root Calculator?

Definition: This calculator computes the fifth root (\( \sqrt[5]{a} \)) or any nth root (\( \sqrt[n]{a} \)) of a real number \( a \), given the number and the root degree \( n \). The fifth root of a number \( a \) is a value \( b \) such that \( b^5 = a \).

Purpose: It assists in mathematics education, engineering, and scientific calculations where roots are needed, such as solving polynomial equations or analyzing growth rates.

2. How Does the Calculator Work?

The calculator uses the following formula:

nth Root: \( \sqrt[n]{a} = a^{1/n} \).
Fifth Root (when \( n = 5 \)): \( \sqrt[5]{a} = a^{1/5} \).

Handling Negative Numbers:

For odd \( n \) (e.g., \( n = 5 \)), the root of a negative number is real and negative: \( \sqrt[n]{-a} = -\sqrt[n]{a} \).
For even \( n \), the root of a negative number is complex and not supported by this calculator.

Steps:

Input the number \( a \) and the root degree \( n \) (default is 5 for fifth root).
Validate inputs: \( n \) must be a positive integer; \( a \) cannot be negative for even \( n \).
Compute the root using the exponentiation formula.
Format the output to 4 decimal places or scientific notation for small values.

3. Importance of Fifth Root Calculations

Calculating the fifth root is important for:

Mathematics Education: Understanding roots as the inverse of exponentiation.
Engineering: Solving equations involving fifth powers, such as in structural analysis.
Finance and Science: Modeling phenomena with non-linear growth or decay.

4. Using the Calculator

Examples:

Example 1: Fifth root of \( a = 7776 \)
- Input: \( a = 7776 \), \( n = 5 \).
- Calculation: \( \sqrt[5]{7776} = 7776^{1/5} \approx 6 \).
- Verification: \( 6^5 = 6 \cdot 6 \cdot 6 \cdot 6 \cdot 6 = 7776 \).
- Output: \( 6.0000 \).
Example 2: Fifth root of \( a = -32 \)
- Input: \( a = -32 \), \( n = 5 \).
- Calculation: \( \sqrt[5]{-32} = - (32^{1/5}) \approx -2 \).
- Verification: \( (-2)^5 = -2 \cdot -2 \cdot -2 \cdot -2 \cdot -2 = -32 \).
- Output: \( -2.0000 \).
Example 3: Third root of \( a = 512 \)
- Input: \( a = 512 \), \( n = 3 \).
- Calculation: \( \sqrt[3]{512} = 512^{1/3} \approx 8 \).
- Verification: \( 8^3 = 8 \cdot 8 \cdot 8 = 512 \).
- Output: \( 8.0000 \).

5. Frequently Asked Questions (FAQ)

Q: What is a fifth root?
A: The fifth root of a number \( a \) is a value \( b \) such that \( b^5 = a \). For example, the fifth root of 243 is 3 because \( 3^5 = 243 \).

Q: Can the fifth root of a negative number be calculated?
A: Yes, the fifth root of a negative number is real and negative because 5 is an odd number. For example, \( \sqrt[5]{-32} = -2 \).

Q: How is the fifth root related to exponentiation?
A: The fifth root is the inverse operation of raising a number to the fifth power. Mathematically, \( \sqrt[5]{a} = a^{1/5} \).