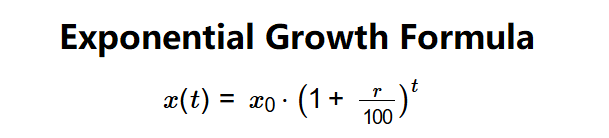Exponential Growth Calculator

1. What is an Exponential Growth Calculator?

Definition: This calculator computes the final value \( x(t) \) of a quantity undergoing exponential growth or decay, given the initial value \( x_0 \), the rate of change \( r \) (as a percentage), and the elapsed time \( t \) in various units (seconds, minutes, hours, days, weeks, months, years). It uses the exponential growth formula to model processes like population growth, investment growth, or decay.

Purpose: It aids in mathematics, finance, biology, and other fields by predicting future values based on exponential growth or decay rates, useful for modeling real-world phenomena over different time scales.

2. How Does the Calculator Work?

The calculator uses the following exponential growth formula:

Exponential Growth: \( x(t) = x_0 \cdot \left(1 + \frac{r}{100}\right)^t \)

Steps:

Input the initial value \( x_0 \), rate of change \( r \) (in percentage), elapsed time \( t \), and select the time unit (seconds, minutes, hours, days, weeks, months, years).
Validate inputs (\( x_0 \geq 0 \), \( t \geq 0 \); \( r \) can be any real number).
Convert the elapsed time \( t \) to years based on the selected unit.
Compute the growth factor \( 1 + \frac{r}{100} \).
Calculate the final value \( x(t) \) using the formula, with \( t \) in years.
Format the output to 4 decimal places or scientific notation for very small or large values.

3. Importance of Exponential Growth Calculations

Exponential growth calculations are essential for:

Finance: Calculating compound interest or investment growth over varying time periods.
Biology: Modeling population growth or the spread of diseases over days, months, or years.
Physics and Chemistry: Describing processes like radioactive decay (with negative \( r \)) or chemical reactions over short or long time scales.

4. Using the Calculator

Examples:

Growth Over Years: Initial value \( x_0 = 100 \), Rate \( r = 5 \), Time \( t = 2 \) years
\( x(t) = 100 \cdot \left(1 + \frac{5}{100}\right)^2 = 100 \cdot 1.05^2 = 100 \cdot 1.1025 = 110.2500 \).
Decay Over Months: Initial value \( x_0 = 200 \), Rate \( r = -10 \), Time \( t = 6 \) months
Convert time: \( t = 6 \div 12 = 0.5 \) years
\( x(t) = 200 \cdot \left(1 + \frac{-10}{100}\right)^{0.5} = 200 \cdot 0.9^{0.5} \approx 200 \cdot 0.9487 = 189.7377 \).
Growth Over Days: Initial value \( x_0 = 50 \), Rate \( r = 2 \), Time \( t = 730 \) days
Convert time: \( t = 730 \div 365 = 2 \) years
\( x(t) = 50 \cdot \left(1 + \frac{2}{100}\right)^2 = 50 \cdot 1.02^2 = 50 \cdot 1.0404 = 52.0200 \).

5. Frequently Asked Questions (FAQ)

Q: What is exponential growth?
A: Exponential growth occurs when a quantity increases at a rate proportional to its current value, modeled by the formula \( x(t) = x_0 \cdot \left(1 + \frac{r}{100}\right)^t \), where \( t \) can be in various time units.

Q: How does the time unit affect the calculation?
A: The elapsed time \( t \) is converted to years based on the selected unit (e.g., 1 year = 12 months, 365 days, etc.), and the growth factor is applied over that time period.

Q: Can the rate of change be negative?
A: Yes, a negative rate of change \( r \) results in exponential decay, where the quantity decreases over time.