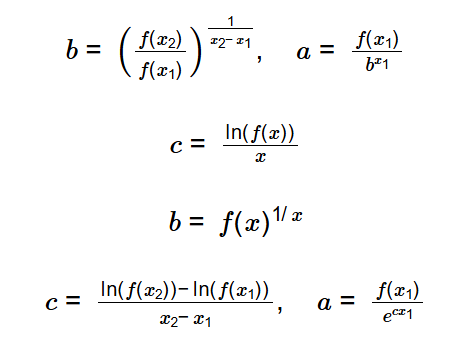Exponential Function Calculator

Function Type:

Enter Two Points

\( x_1 \):

\( f(x_1) \):

\( x_2 \):

\( f(x_2) \):

1. What is an Exponential Function Calculator?

Definition: This calculator determines the parameters of exponential functions such as \( a b^x \), \( e^{cx} \), \( b^x \), or \( a e^{cx} \). The user inputs points on the function and/or known parameters, and the calculator solves for the unknown parameters.

Purpose: It aids in mathematics education, modeling, and scientific applications by fitting exponential functions to data points, useful in growth modeling, physics, and finance.

2. How Does the Calculator Work?

The calculator uses the following exponential functions and solves for parameters:

For \( f(x) = a b^x \), two points: \( b = \left( \frac{f(x_2)}{f(x_1)} \right)^{\frac{1}{x_2 - x_1}}, \quad a = \frac{f(x_1)}{b^{x_1}} \)
For \( f(x) = e^{cx} \), one point: \( c = \frac{\ln(f(x))}{x} \)
For \( f(x) = b^x \), one point: \( b = f(x)^{1/x} \)
For \( f(x) = a e^{cx} \), two points: \( c = \frac{\ln(f(x_2)) - \ln(f(x_1))}{x_2 - x_1}, \quad a = \frac{f(x_1)}{e^{c x_1}} \)

Steps:

Select the function type (\( a b^x \), \( e^{cx} \), \( b^x \), or \( a e^{cx} \)).
Input the required points and/or parameters based on the function type.
Validate inputs (points must be distinct, function values must be positive).
Compute the unknown parameters using the appropriate formulas.
Format the output to 4 decimal places or scientific notation for very small or large values.

3. Importance of Exponential Function Calculations

Exponential function calculations are essential for:

Mathematics Education: Understanding exponential functions and their parameters.
Science and Engineering: Modeling exponential growth/decay in physics, biology, or electronics.
Data Analysis: Fitting exponential models to data in finance (compound interest) or epidemiology (disease spread).

4. Using the Calculator

Examples:

Function \( a b^x \), Two Points: \( (x_1 = 1, f(x_1) = 6) \), \( (x_2 = 3, f(x_2) = 24) \)
\( b = \left( \frac{24}{6} \right)^{\frac{1}{3-1}} = 4^{1/2} = 2 \), \( a = \frac{6}{2^1} = 3 \)
Result: \( a = 3.0000 \), \( b = 2.0000 \).
Function \( e^{cx} \), One Point: \( (x = 2, f(x) = 7.3891) \)
\( c = \frac{\ln(7.3891)}{2} \approx \frac{2}{2} = 1 \)
Result: \( c = 1.0000 \).
Function \( b^x \), One Point: \( (x = 3, f(x) = 8) \)
\( b = 8^{1/3} = 2 \)
Result: \( b = 2.0000 \).

5. Frequently Asked Questions (FAQ)

Q: What is an exponential function?
A: An exponential function is of the form \( f(x) = a b^x \), where \( a \) is a coefficient, \( b \) is the base, and \( x \) is the exponent, commonly used to model growth or decay.

Q: Why must the function values be positive?
A: For real solutions, function values must be positive because logarithms and roots are defined for positive numbers in the real number system.

Q: Why do some functions require two points?
A: Functions with two parameters (e.g., \( a \) and \( b \)) require two points to provide enough equations to solve for both unknowns.