Exponent Calculator

1. What is an Exponent Calculator?

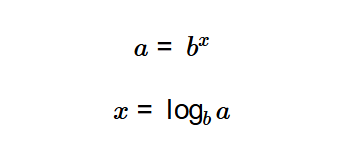
Definition: This calculator computes one variable in the exponential equation \( b^x = a \), where \( b \) is the base, \( x \) is the exponent, and \( a \) is the result. The user inputs any two of these values, and the calculator solves for the third.

Purpose: It aids in mathematics education, algebra, and scientific calculations by solving exponential equations, useful in areas like growth modeling, physics, and finance.

2. How Does the Calculator Work?

The calculator uses the following exponential relationships:

Given Base and Exponent: \( a = b^x \)
Given Base and Result: \( x = \log_b a \)
Given Exponent and Result: \( b = a^{1/x} \)

Steps:

Input any two of Base \( b \), Exponent \( x \), and Result \( a \), leaving the third field blank.
Validate inputs (exactly two fields filled; \( b > 0 \), \( b \neq 1 \), \( a > 0 \), \( x \neq 0 \)).
Determine which variable to calculate based on the blank field.
Compute the missing variable using the appropriate formula.
Format the output to 4 decimal places or scientific notation for very small or large values.

3. Importance of Exponent Calculations

Exponent calculations are essential for:

Mathematics Education: Understanding exponential functions and their inverses (logarithms).
Science and Engineering: Modeling exponential growth/decay in physics, biology, or electronics.
Finance: Calculating compound interest or exponential growth rates.

4. Using the Calculator

Examples:

Calculate Result: Base \( b = 2 \), Exponent \( x = 3 \)
Result: \( a = 2^3 = 8.0000 \).
Calculate Exponent: Base \( b = 10 \), Result \( a = 100 \)
Exponent: \( x = \log_{10} 100 = 2.0000 \).
Calculate Base: Exponent \( x = 2 \), Result \( a = 16 \)
Base: \( b = 16^{1/2} = 4.0000 \).

5. Frequently Asked Questions (FAQ)

Q: What does \( b^x = a \) represent?
A: It represents an exponential equation where \( b \) is the base, \( x \) is the exponent, and \( a \) is the result. The calculator solves for one variable given the other two.

Q: Why can’t the base be 1 when calculating the exponent?
A: The logarithm with base 1 is undefined because \( 1^x = 1 \) for all \( x \), so it cannot produce a unique exponent.

Q: Can the result be negative?
A: No, the result \( a \) must be positive for real solutions when calculating \( x \) or \( b \), as logarithms and roots are defined for positive numbers in the real number system.