Ellipsoid Volume Calculator - Find V from Semi-axes A, B, C

Semi-axis \( a \):

Semi-axis \( b \):

Semi-axis \( c \):

1. What is an Ellipsoid Volume Calculator?

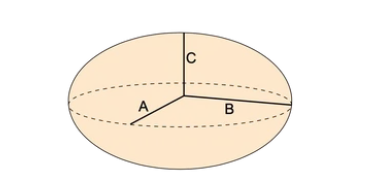
Definition: This calculator determines the volume of an ellipsoid based on the lengths of its three semi-axes (\( a \), \( b \), \( c \)). An ellipsoid is a three-dimensional geometric shape where each cross-section is an ellipse, often described as a stretched or compressed sphere.

Purpose: It assists in calculating volumes for applications in geometry, physics, and engineering, such as determining the capacity of ellipsoid-shaped containers or modeling objects in scientific studies.

2. How Does the Calculator Work?

The calculator uses the following formula:

Volume \( V \): \( V = \frac{4}{3} \pi a b c \).

Unit Conversions:

Length Units: m, cm (1 m = 100 cm), mm (1 m = 1000 mm), in (1 m = 39.3701 in), ft (1 m = 3.28084 ft), yd (1 m = 1.09361 yd).
Volume Units: m³, cm³ (1 m³ = 1000000 cm³), mm³ (1 m³ = 1000000000 mm³), in³ (1 m³ = 61023.7441 in³), ft³ (1 m³ = 35.3147 ft³), yd³ (1 m³ = 1.30795 yd³).

Steps:

Enter the semi-axes lengths \( a \), \( b \), and \( c \) and select their units.
Validate the inputs (must be positive).
Convert inputs to meters for calculations.
Compute the volume using the formula above.
Convert the output to the selected unit.
Format the output to 4 decimal places or scientific notation for small values.

3. Importance of Ellipsoid Volume Calculations

Calculating ellipsoid volumes is crucial for:

Mathematics Education: Teaching properties of three-dimensional shapes.
Engineering Design: Creating ellipsoid structures like tanks or domes.
Scientific Research: Modeling objects in physics or biology, such as cells or celestial bodies.

4. Using the Calculator

Examples:

Example 1: Semi-axes \( a = 10 \, \text{cm} \), \( b = 6 \, \text{cm} \), \( c = 8 \, \text{cm} \)
- Convert: \( a = 0.1 \, \text{m} \), \( b = 0.06 \, \text{m} \), \( c = 0.08 \, \text{m} \).
- Volume: \( V = \frac{4}{3} \pi \times 0.1 \times 0.06 \times 0.08 \approx 0.0020106 \, \text{m}^3 = 2010.6193 \, \text{cm}^3 \).
Example 2: Semi-axes \( a = 3 \, \text{m} \), \( b = 2 \, \text{m} \), \( c = 1.5 \, \text{m} \)
- Volume: \( V = \frac{4}{3} \pi \times 3 \times 2 \times 1.5 \approx 37.6991 \, \text{m}^3 \).

5. Frequently Asked Questions (FAQ)

Q: What is an ellipsoid?
A: An ellipsoid is a three-dimensional shape with three unequal semi-axes, where all cross-sections are ellipses. If all semi-axes are equal, it becomes a sphere.

Q: How does an ellipsoid differ from a sphere?
A: A sphere has equal radii in all directions (\( a = b = c \)), while an ellipsoid has three distinct semi-axes (\( a \), \( b \), \( c \)), allowing it to be stretched or compressed.

Q: Why is the volume formula \( \frac{4}{3} \pi a b c \)?
A: The formula generalizes the sphere’s volume (\( V = \frac{4}{3} \pi r^3 \)) by multiplying the semi-axes \( a \), \( b \), and \( c \), accounting for the ellipsoid’s shape.