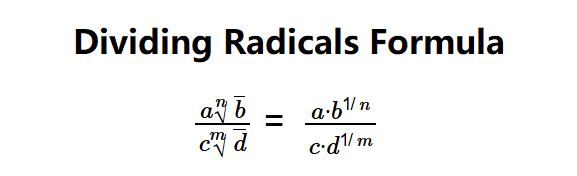Dividing Radicals Calculator

First Factor (\( a \sqrt[n]{b} \))

Coefficient \( a \):

Radicand \( b \):

Index \( n \):

Second Factor (\( c \sqrt[m]{d} \))

Coefficient \( c \):

Radicand \( d \):

Index \( m \):

1. What is a Dividing Radicals Calculator?

Definition: This calculator computes the quotient of two radical expressions, \( \frac{a \sqrt[n]{b}}{c \sqrt[m]{d}} \), given the coefficients \( a \) and \( c \), radicands \( b \) and \( d \), and indices \( n \) and \( m \). It simplifies the division by converting radicals to exponents and evaluating the result numerically.

Purpose: It aids in mathematics education, algebra, and scientific calculations by simplifying the division of radical expressions, useful in geometry, physics, and engineering problems.

2. How Does the Calculator Work?

The calculator uses the following approach:

General Division: \( \frac{a \sqrt[n]{b}}{c \sqrt[m]{d}} = \frac{a \cdot b^{1/n}}{c \cdot d^{1/m}} \)

Steps:

Input the coefficients \( a \) and \( c \), radicands \( b \) and \( d \), and indices \( n \) and \( m \).
Validate inputs (\( b \geq 0 \), \( d \geq 0 \), \( n \neq 0 \), \( m \neq 0 \), \( c \neq 0 \)).
Convert radicals to exponents: \( \sqrt[n]{b} = b^{1/n} \), \( \sqrt[m]{d} = d^{1/m} \).
Compute the expression: \( \frac{a \cdot b^{1/n}}{c \cdot d^{1/m}} \).
Format the output to 4 decimal places or scientific notation for very small or large values.

3. Importance of Dividing Radicals

Dividing radicals is essential for:

Mathematics Education: Understanding properties of radicals and exponents.
Geometry: Simplifying expressions involving areas, volumes, or lengths (e.g., simplifying \( \sqrt{8} / \sqrt{2} \)).
Physics and Engineering: Handling radical expressions in equations for wave frequencies, electrical circuits, or scaling laws.

4. Using the Calculator

Examples:

Example 1: First factor: \( a = 2 \), \( b = 16 \), \( n = 4 \); Second factor: \( c = 3 \), \( d = 81 \), \( m = 4 \)
Expression: \( \frac{2 \sqrt[4]{16}}{3 \sqrt[4]{81}} = \frac{2 \cdot 16^{1/4}}{3 \cdot 81^{1/4}} = \frac{2 \cdot 2}{3 \cdot 3} = \frac{4}{9} \approx 0.4444 \).
Example 2: First factor: \( a = 1 \), \( b = 25 \), \( n = 2 \); Second factor: \( c = 1 \), \( d = 4 \), \( m = 2 \)
Expression: \( \frac{\sqrt{25}}{\sqrt{4}} = \frac{25^{1/2}}{4^{1/2}} = \frac{5}{2} = 2.5000 \).
Example 3: First factor: \( a = 5 \), \( b = 8 \), \( n = 3 \); Second factor: \( c = 2 \), \( d = 27 \), \( m = 3 \)
Expression: \( \frac{5 \sqrt[3]{8}}{2 \sqrt[3]{27}} = \frac{5 \cdot 8^{1/3}}{2 \cdot 27^{1/3}} = \frac{5 \cdot 2}{2 \cdot 3} = \frac{5}{3} \approx 1.6667 \).

5. Frequently Asked Questions (FAQ)

Q: What does dividing radicals mean?
A: Dividing radicals means computing the quotient of two radical expressions, \( \frac{a \sqrt[n]{b}}{c \sqrt[m]{d}} \), by converting radicals to exponents and evaluating the result.

Q: Why can’t the denominator coefficient be zero?
A: The denominator coefficient \( c \) cannot be zero because it results in division by zero, which is undefined.

Q: Can the radicands be negative?
A: No, in the real number system, radicands must be non-negative to ensure the radicals are defined (unless the index is an odd integer, but this calculator assumes real results).