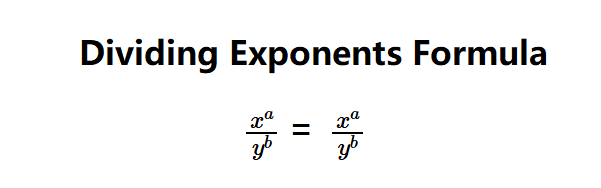Dividing Exponents Calculator

1. What is a Dividing Exponents Calculator?

Definition: This calculator computes the quotient of two exponential expressions, \( \frac{x^a}{y^b} \), given the bases \( x \) and \( y \), and exponents \( a \) and \( b \). It handles both cases where the bases are the same or different, simplifying the expression using exponent rules or numerical computation.

Purpose: It aids in mathematics education, algebra, and scientific calculations by simplifying division of exponential expressions, useful in fields like physics, engineering, and finance.

2. How Does the Calculator Work?

The calculator uses the following exponent rules:

Same Bases: \( \frac{x^a}{x^b} = x^{a-b} \)
Different Bases: \( \frac{x^a}{y^b} = \frac{x^a}{y^b} \) (computed numerically or simplified via prime factorization)

Steps:

Input the bases \( x \) and \( y \), and exponents \( a \) and \( b \).
Validate inputs (\( x \neq 0 \), \( y \neq 0 \); exponents can be any real numbers).
If bases are the same, apply the quotient rule: \( x^{a-b} \).
If bases are different, compute \( x^a \) and \( y^b \), then divide: \( \frac{x^a}{y^b} \).
Format the output to 4 decimal places or scientific notation for very small or large values.

3. Importance of Dividing Exponents

Dividing exponents is essential for:

Mathematics Education: Understanding exponent rules and simplifying expressions.
Science and Engineering: Simplifying calculations in exponential growth, decay, or scaling laws.
Data Analysis: Handling exponential data in fields like finance (compound interest) or biology (population growth).

4. Using the Calculator

Examples:

Same Bases: Base \( x = 7 \), Exponent \( a = 5 \), Base \( y = 7 \), Exponent \( b = 3 \)
Result: \( \frac{7^5}{7^3} = 7^{5-3} = 7^2 = 49.0000 \).
Different Bases: Base \( x = 15 \), Exponent \( a = 4 \), Base \( y = 12 \), Exponent \( b = 6 \)
Result: \( \frac{15^4}{12^6} = \frac{50625}{2985984} \approx 0.01695 \).
Negative Exponent: Base \( x = 7 \), Exponent \( a = -8 \), Base \( y = 7 \), Exponent \( b = -6 \)
Result: \( \frac{7^{-8}}{7^{-6}} = 7^{-8-(-6)} = 7^{-2} = \frac{1}{7^2} = \frac{1}{49} \approx 0.0204 \).

5. Frequently Asked Questions (FAQ)

Q: What is dividing exponents?
A: Dividing exponents means computing the quotient of two exponential expressions, \( \frac{x^a}{y^b} \), either by subtracting exponents (same bases) or computing numerically (different bases).

Q: What happens if the bases are the same?
A: If the bases are the same, subtract the exponents: \( \frac{x^a}{x^b} = x^{a-b} \).

Q: Can the bases be zero?
A: No, the denominator base \( y \) cannot be zero (division by zero). The numerator base \( x \) can be zero only if the exponent \( a \leq 0 \), but this is typically undefined for \( 0^0 \).