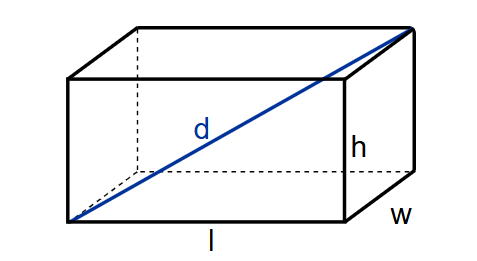
1. What is a Cuboid Calculator?
Definition: This calculator computes the surface area, volume, and space diagonal of a cuboid, given its length \( l \), width \( w \), and height \( h \). A cuboid is a three-dimensional shape with six rectangular faces, where opposite faces are equal. The calculator allows inputs in various units (feet, inches, yards, cm, m), defaulting to feet, and provides outputs with flexible unit conversions: surface area (default: square feet), volume (default: cubic feet), and diagonal (default: feet).
Purpose: It aids in practical applications by calculating key properties of cuboids, useful in fields like architecture, construction, and storage for designing rooms, calculating material needs, or determining container capacities.
2. How Does the Calculator Work?
The calculator uses the following formulas:
- Surface Area: \( 2(lw + lh + wh) \)
- Volume: \( V = l \times w \times h \)
- Space Diagonal: \( d = \sqrt{l^2 + w^2 + h^2} \)
Steps:
- Input the length \( l \), width \( w \), and height \( h \) with their units (default: feet).
- Validate that all inputs are positive.
- Convert the inputs to feet for calculation.
- Compute the surface area, volume, and space diagonal in feet-based units.
- Convert the outputs to the user-selected units (surface area: sq ft, volume: cu ft, diagonal: ft by default).
- Display the results to 4 decimal places.
3. Importance of Cuboid Calculations
Cuboid calculations are essential for:
- Architecture: Designing rooms or buildings, calculating surface area for painting or flooring, and volume for capacity.
- Construction: Estimating material quantities (e.g., concrete, drywall), often requiring unit conversions (e.g., feet to meters).
- Storage: Determining the capacity of rectangular containers, such as shipping boxes or storage units.
4. Using the Calculator
Examples:
- Example 1: Length \( l = 5 \) ft, Width \( w = 3 \) ft, Height \( h = 2 \) ft, Outputs in sq ft, cu ft, ft
Surface Area: \( 2(5 \times 3 + 5 \times 2 + 3 \times 2) = 62.0000 \) sq ft,
Volume: \( 5 \times 3 \times 2 = 30.0000 \) cu ft,
Diagonal: \( \sqrt{5^2 + 3^2 + 2^2} \approx 6.1644 \) ft.
- Example 2: Length \( l = 48 \) in, Width \( w = 36 \) in, Height \( h = 24 \) in, Outputs in sq in, cu in, in
Convert to feet: \( l = 48 / 12 = 4 \) ft, \( w = 36 / 12 = 3 \) ft, \( h = 24 / 12 = 2 \) ft,
Surface Area: \( 2(4 \times 3 + 4 \times 2 + 3 \times 2) = 52.0000 \) sq ft = 7488.0000 sq in,
Volume: \( 4 \times 3 \times 2 = 24.0000 \) cu ft = 41472.0000 cu in,
Diagonal: \( \sqrt{4^2 + 3^2 + 2^2} \approx 5.3852 \) ft = 64.6218 in.
- Example 3: Length \( l = 2 \) m, Width \( w = 1.5 \) m, Height \( h = 1 \) m, Outputs in sq m, cu m, m
Convert to feet: \( l = 2 \times 3.28084 \approx 6.5617 \) ft, \( w = 1.5 \times 3.28084 \approx 4.9213 \) ft, \( h = 1 \times 3.28084 \approx 3.28084 \) ft,
Surface Area: \( 2(6.5617 \times 4.9213 + 6.5617 \times 3.28084 + 4.9213 \times 3.28084) \approx 99.2145 \) sq ft = 9.2197 sq m,
Volume: \( 6.5617 \times 4.9213 \times 3.28084 \approx 105.9449 \) cu ft = 3.0000 cu m,
Diagonal: \( \sqrt{(6.5617)^2 + (4.9213)^2 + (3.28084)^2} \approx 8.7596 \) ft = 2.6699 m.
- Example 4: Length \( l = 2 \) yd, Width \( w = 1 \) yd, Height \( h = 1 \) yd, Outputs in sq yd, cu yd, yd
Convert to feet: \( l = 2 \times 3 = 6 \) ft, \( w = 1 \times 3 = 3 \) ft, \( h = 1 \times 3 = 3 \) ft,
Surface Area: \( 2(6 \times 3 + 6 \times 3 + 3 \times 3) = 72.0000 \) sq ft = 8.0000 sq yd,
Volume: \( 6 \times 3 \times 3 = 54.0000 \) cu ft = 2.0000 cu yd,
Diagonal: \( \sqrt{6^2 + 3^2 + 3^2} \approx 7.3485 \) ft = 2.4495 yd.
5. Frequently Asked Questions (FAQ)
Q: Why do inputs default to feet?
A: Feet are the default unit as they are commonly used in many practical applications like construction and storage. You can switch to other units using the dropdowns.
Q: Why must the length, width, and height be positive?
A: These dimensions represent physical measurements of a cuboid, which must be positive to define a valid shape.
Q: What is the space diagonal of a cuboid?
A: The space diagonal is the straight line connecting two opposite vertices of the cuboid, passing through its interior. It’s calculated using the formula \( \sqrt{l^2 + w^2 + h^2} \), and it represents the longest straight-line distance within the cuboid.
 Home
Home
 Back
Back