1. What is a Cube Surface Area Calculator?
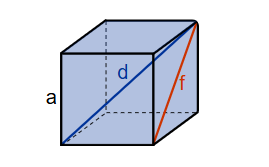
Definition: This calculator computes the cube diagonal (\( d \)), face diagonal (\( f \)), volume, and surface area of a cube, given the side length (\( a \)). A cube is a three-dimensional shape with six identical square faces of equal length, making it a highly regular polyhedron.
Purpose: It aids in geometry education, engineering, and design by calculating key parameters for applications like packaging (e.g., cubic containers), architecture (e.g., cubic structures), and material estimation.[](https://www.omnicalculator.com/math/cube-surface-area)
2. How Does the Calculator Work?
The calculator takes the side length (\( a \)) with a selected unit (m, cm, mm, in, ft, yd) and computes:
- Cube Diagonal (\( d \)):
- Formula: \( d = a \sqrt{3} \).
- The diagonal across the cube, from one vertex to the opposite vertex.
- Face Diagonal (\( f \)):
- Formula: \( f = a \sqrt{2} \).
- The diagonal of a square face, connecting opposite vertices of one face.
- Volume:
- Formula: \( V = a^3 \).
- The space occupied by the cube, calculated as the side length cubed.
- Surface Area:
- Formula: \( A = 6a^2 \).
- The total area of the six square faces, each with area \( a^2 \).
Unit Conversions:
- Length Units: m, cm (1 m = 100 cm), mm (1 m = 1000 mm), in (1 m = 39.3701 in), ft (1 m = 3.28084 ft), yd (1 m = 1.09361 yd).
- Volume Units: m³, cm³ (1 m³ = 1000000 cm³), mm³ (1 m³ = 1000000000 mm³), in³ (1 m³ = 61023.7441 in³), ft³ (1 m³ = 35.3147 ft³), yd³ (1 m³ = 1.30795 yd³).
- Area Units: m², cm² (1 m² = 10000 cm²), mm² (1 m² = 1000000 mm²), in² (1 m² = 1550.0031 in²), ft² (1 m² = 10.7639 ft²), yd² (1 m² = 1.19599 yd²).
Steps:
- Input the side length (\( a \)) with its unit.
- Validate input (\( a > 0 \)).
- Convert the side length to meters for calculations.
- Compute cube diagonal, face diagonal, volume, and surface area.
- Convert each result to its independently selected output unit and format to 4 decimal places or scientific notation for small values.
3. Importance of Cube Surface Area Calculations
Calculating cube parameters is crucial for:
- Geometry Education: Understanding the properties of regular polyhedra and their symmetry.
- Engineering and Manufacturing: Designing cubic containers, dice, or structural components, and estimating material requirements.
- Packaging and Logistics: Optimizing space usage, as cubes can fill 3D space without gaps, maximizing efficiency.[](https://www.omnicalculator.com/math/cube-v-a-d)
4. Using the Calculator
Examples:
- Example 1: Side \( a = 4 \, \text{cm} \), Output units: cm, cm, cm³, cm²
Convert: \( a = 0.04 \, \text{m} \).
Cube Diagonal: \( d = 0.04 \times \sqrt{3} \approx 0.0693 \, \text{m} = 6.9282 \, \text{cm} \).
Face Diagonal: \( f = 0.04 \times \sqrt{2} \approx 0.0566 \, \text{m} = 5.6569 \, \text{cm} \).
Volume: \( V = 0.04^3 = 0.000064 \, \text{m}^3 = 64.0000 \, \text{cm}^3 \).
Surface Area: \( A = 6 \times 0.04^2 = 0.0096 \, \text{m}^2 = 96.0000 \, \text{cm}^2 \).
- Example 2: Side \( a = 2 \, \text{m} \), Output units: m, ft, m³, ft²
Cube Diagonal: \( d = 2 \times \sqrt{3} \approx 3.4641 \, \text{m} \).
Face Diagonal: \( f = 2 \times \sqrt{2} \approx 2.8284 \, \text{m} = 9.2830 \, \text{ft} \).
Volume: \( V = 2^3 = 8.0000 \, \text{m}^3 \).
Surface Area: \( A = 6 \times 2^2 = 24.0000 \, \text{m}^2 = 258.3336 \, \text{ft}^2 \).
- Example 3: Side \( a = 10 \, \text{in} \), Output units: mm, in, in³, mm²
Convert: \( a = 0.2540 \, \text{m} \).
Cube Diagonal: \( d \approx 0.4398 \, \text{m} = 439.8230 \, \text{mm} \).
Face Diagonal: \( f \approx 0.3591 \, \text{m} = 14.1372 \, \text{in} \).
Volume: \( V \approx 0.0164 \, \text{m}^3 = 1000.0000 \, \text{in}^3 \).
Surface Area: \( A \approx 0.3871 \, \text{m}^2 = 387096.7742 \, \text{mm}^2 \).
5. Frequently Asked Questions (FAQ)
Q: What is a cube?
A: A cube is a three-dimensional shape with six identical square faces of equal length, making all edges and faces congruent.
Q: Why is the surface area formula \( 6a^2 \)?
A: Each face of a cube is a square with area \( a^2 \), and a cube has six faces, so the total surface area is six times the area of one face.
Q: Can I use different units for each output?
A: Yes, the calculator allows independent unit selection for cube diagonal, face diagonal, volume, and surface area, enabling flexible conversions (e.g., diagonal in meters, volume in cubic inches).
 Home
Home
 Back
Back