1. What is a Cosh Calculator?

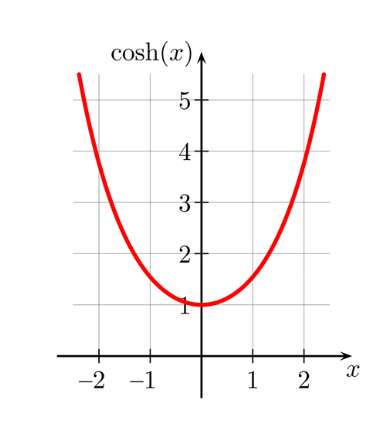
Definition: This calculator computes the hyperbolic cosine (\( \cosh(x) \)) and related hyperbolic functions (\( \sinh(x) \), \( \tanh(x) \), \( \coth(x) \), \( \sech(x) \), \( \csch(x) \)) for a given input \( x \). These functions are defined using exponential functions and are used in physics, engineering, and mathematics to model phenomena like catenary curves and wave equations. The input \( x \) can be in degrees or radians (defaulting to radians).

Purpose: It aids in mathematical education and practical applications by simplifying the calculation of hyperbolic function values, useful in fields like engineering (e.g., designing suspension bridges), physics (e.g., wave propagation), and advanced mathematics.

2. How Does the Calculator Work?

The calculator uses the following definitions for hyperbolic functions:

• \( \cosh(x) = \frac{e^x + e^{-x}}{2} \)
• \( \sinh(x) = \frac{e^x - e^{-x}}{2} \)
• \( \tanh(x) = \frac{\sinh(x)}{\cosh(x)} = \frac{e^x - e^{-x}}{e^x + e^{-x}} \)

If the input \( x \) is in degrees, it is converted to radians using: \( x_{\text{radians}} = x_{\text{degrees}} \times \frac{\pi}{180} \)

For results with an absolute value less than 0.0001, the calculator displays them in scientific notation.

Steps:

• Input a value \( x \) and select its unit (degrees or radians, defaulting to radians).
• Convert \( x \) to radians if necessary.
• Validate that \( x \neq 0 \) for \( \coth(x) \) and \( \csch(x) \), as they are undefined at \( x = 0 \).
• Compute \( \cosh(x) \), \( \sinh(x) \), \( \tanh(x) \), \( \coth(x) \), \( \sech(x) \), and \( \csch(x) \).
• Format results: use scientific notation if the absolute value is less than 0.0001, otherwise display to 4 decimal places.

3. Importance of Cosh Calculations

Hyperbolic function calculations are essential for:

• Engineering: Modeling the shape of a hanging cable or chain (catenary curve), as seen in suspension bridges or power lines.
• Physics: Describing wave propagation, such as in the Klein-Gordon equation, or in special relativity for Lorentz transformations.
• Mathematics: Solving differential equations where hyperbolic functions naturally arise, or in complex analysis.

4. Using the Calculator

Examples:

• Example 1: \( x = 0 \) radians
  \( \cosh(0) = \frac{e^0 + e^{-0}}{2} = 1.0000 \),
  \( \sinh(0) = \frac{e^0 - e^{-0}}{2} = 0.0000 \),
  \( \tanh(0) = \frac{0}{1} = 0.0000 \),
  
• Example 2: \( x = 1 \) radian
  \( \cosh(1) \approx 1.5431 \),
  \( \sinh(1) \approx 1.1752 \),
  \( \tanh(1) \approx 0.7616 \),
  
• Example 3: \( x = 60^\circ \) (convert to radians: \( 60 \times \frac{\pi}{180} \approx 1.0472 \))
  \( \cosh(1.0472) \approx 1.6003 \),
  \( \sinh(1.0472) \approx 1.2494 \),
  \( \tanh(1.0472) \approx 0.7807 \),
  
• Example 4: \( x = -10 \) radians (to demonstrate scientific notation for small values)
  \( \cosh(-10) = \cosh(10) \approx 11013.2329 \),
  \( \sinh(-10) \approx -11013.2329 \),
  \( \tanh(-10) \approx -1.0000 \),
  

5. Frequently Asked Questions (FAQ)

Q: What is the difference between \( \cosh(x) \) and \( \cos(x) \)?
A: While \( \cos(x) \) is a trigonometric function related to circles and periodic phenomena, \( \cosh(x) \) is a hyperbolic function related to hyperbolas and exponential growth. They share some similar identities, but their definitions and applications differ.

Q: Why does the input default to radians?
A: Radians are the standard unit for mathematical functions like \( \cosh(x) \) in most scientific contexts, as they align naturally with exponential definitions and calculus. However, you can switch to degrees using the dropdown.

Q: Why are \( \coth(x) \) and \( \csch(x) \) undefined at \( x = 0 \)?
A: At \( x = 0 \), \( \sinh(0) = 0 \), and since \( \coth(x) = \frac{\cosh(x)}{\sinh(x)} \) and \( \csch(x) = \frac{1}{\sinh(x)} \), both involve division by zero, making them undefined.

Q: Why are some results displayed in scientific notation?
A: Results with an absolute value less than 0.0001 are displayed in scientific notation to improve readability and precision for very small numbers.

Cosh Calculator© - All Rights Reserved 2025