Cos-1 Calculator

1. What is a Cos-1 Calculator?

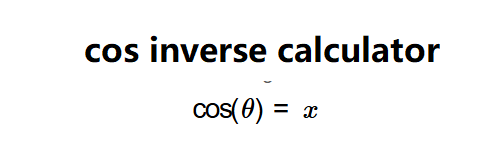
Definition: This calculator computes the inverse cosine (\( \cos^{-1}(x) \), also denoted as \( \arccos(x) \)) of a given value \( x \). The inverse cosine function finds the angle \( \theta \) such that \( \cos(\theta) = x \). The input \( x \) must be between -1 and 1, and the output angle can be displayed in degrees or radians, defaulting to degrees.

Purpose: It aids in trigonometry education and practical applications by calculating the angle corresponding to a cosine value, useful in fields like physics, engineering, and geometry for solving triangles or analyzing periodic phenomena.

2. How Does the Calculator Work?

The calculator uses the inverse cosine function to find the angle \( \theta \) such that:

\( \cos(\theta) = x \)

Domain: \( x \in [-1, 1] \), as the cosine function only takes values between -1 and 1.
Range:

In degrees: \( [0, 180^\circ] \)
In radians: \( [0, \pi] \)

Steps:

Input a value \( x \) between -1 and 1.
Validate the input to ensure it lies within the domain.
Compute \( \cos^{-1}(x) \) in radians using the PHP function acos().
Convert the result to the user-selected unit (degrees or radians).
Display the result to 4 decimal places.

3. Importance of Cos-1 Calculations

Inverse cosine calculations are essential for:

Geometry: Solving triangles using the law of cosines, where you need to find an angle given the sides.
Physics: Determining angles in oscillatory motion or wave analysis, often requiring conversions between degrees and radians.
Engineering: Analyzing angles in structural designs or signal processing.

4. Using the Calculator

Examples:

Example 1: \( x = 1 \), Angle in degrees
Angle: \( \cos^{-1}(1) = 0.0000^\circ \), or 0.0000 radians.
Example 2: \( x = 0 \), Angle in degrees
Angle: \( \cos^{-1}(0) = 90.0000^\circ \), or 1.5708 radians.
Example 3: \( x = -1 \), Angle in radians
Angle: \( \cos^{-1}(-1) = 3.1416 \) radians, or 180.0000 degrees.
Example 4: \( x = \frac{1}{\sqrt{2}} \approx 0.7071 \), Angle in degrees
Angle: \( \cos^{-1}(0.7071) \approx 45.0000^\circ \), or 0.7854 radians.

5. Frequently Asked Questions (FAQ)

Q: Why must the input \( x \) be between -1 and 1?
A: The cosine function only takes values between -1 and 1, so its inverse, \( \cos^{-1}(x) \), is only defined for \( x \in [-1, 1] \). Values outside this range do not correspond to any real angle.

Q: Why does the output default to degrees?
A: Degrees are a common unit in many applications and are more intuitive for most users. However, you can switch to radians using the dropdown.

Q: What is the difference between \( \cos^{-1}(x) \) and \( 1/\cos(x) \)?
A: The notation \( \cos^{-1}(x) \) represents the inverse cosine function (\( \arccos(x) \)), which finds the angle whose cosine is \( x \). In contrast, \( 1/\cos(x) \) is the multiplicative inverse of the cosine function, often denoted as \( \sec(x) \), and is a different concept altogether.