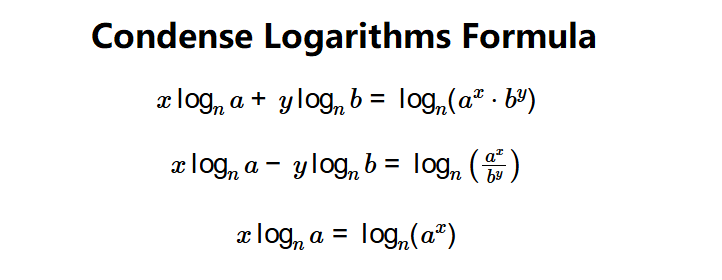Condense Logarithms Calculator

Operation Type:

Coefficient \( x \):

Argument \( a \):

Coefficient \( y \):

Argument \( b \):

Base \( n \):

1. What is a Condense Logarithms Calculator?

Definition: This calculator condenses logarithmic expressions using logarithm properties, combining terms like \( x \log_n a + y \log_n b \), \( x \log_n a - y \log_n b \), or \( x \log_n a \) into a single logarithm with base \( n \). It supports adding logs, subtracting logs, and multiplying a log by a number.

Purpose: It aids in mathematics education and problem-solving by simplifying logarithmic expressions, useful in algebra, calculus, and scientific computations.

2. How Does the Calculator Work?

The calculator uses the following logarithm properties:

Adding Logs: \( x \log_n a + y \log_n b = \log_n (a^x \cdot b^y) \)
Subtracting Logs: \( x \log_n a - y \log_n b = \log_n \left( \frac{a^x}{b^y} \right) \)
A Number Times Log: \( x \log_n a = \log_n (a^x) \)

Steps:

Select the operation type (Adding Logs, Subtracting Logs, A Number Times Log).
Input the coefficients \( x \) and \( y \), arguments \( a \) and \( b \), and base \( n \), as required.
Validate inputs (\( a > 0 \), \( b > 0 \), \( n > 0 \), \( n \neq 1 \); \( x \) and \( y \) can be any real numbers).
Compute the expression inside the logarithm based on the selected operation.
Calculate the final logarithm \( \log_n (\text{expression}) \).
Format the output to 4 decimal places or scientific notation for very small or large values.

3. Importance of Condensing Logarithms

Condensing logarithms is essential for:

Mathematics Education: Simplifying complex logarithmic expressions for easier computation.
Science and Engineering: Handling logarithmic equations in fields like acoustics (decibels), chemistry (pH), or signal processing.
Problem Solving: Streamlining equations in algebra or calculus by reducing multiple logarithmic terms into a single term.

4. Using the Calculator

Examples:

Adding Logs: \( x = 2 \), \( a = 3 \), \( y = 1 \), \( b = 5 \), Base \( n = 10 \)
Expression: \( 2 \log_{10} 3 + 1 \log_{10} 5 = \log_{10} (3^2 \cdot 5^1) = \log_{10} (9 \cdot 5) = \log_{10} 45 \approx 1.6532 \).
Subtracting Logs: \( x = 1 \), \( a = 100 \), \( y = 2 \), \( b = 10 \), Base \( n = 10 \)
Expression: \( 1 \log_{10} 100 - 2 \log_{10} 10 = \log_{10} \left( \frac{100^1}{10^2} \right) = \log_{10} \left( \frac{100}{100} \right) = \log_{10} 1 = 0.0000 \).
A Number Times Log: \( x = 3 \), \( a = 2 \), Base \( n = 2 \)
Expression: \( 3 \log_2 2 = \log_2 (2^3) = \log_2 8 = 3.0000 \).

5. Frequently Asked Questions (FAQ)

Q: What does it mean to condense logarithms?
A: Condensing logarithms means combining multiple logarithmic terms into a single logarithm using properties like the product rule, quotient rule, or power rule.

Q: Why can’t the base be 1?
A: The logarithm with base 1 is undefined because \( 1^y = 1 \) for all \( y \), so it cannot produce a unique value.

Q: Can the arguments be negative?
A: No, the arguments \( a \) and \( b \) must be positive, as logarithms are defined only for positive numbers in the real number system.