Coin Rotation Paradox Calculator

Diameter of the Fixed Coin:

Diameter of the Rotating Coin:

1. What is a Coin Rotation Paradox Calculator?

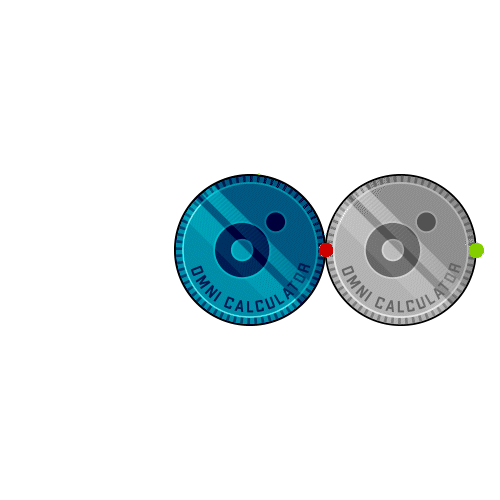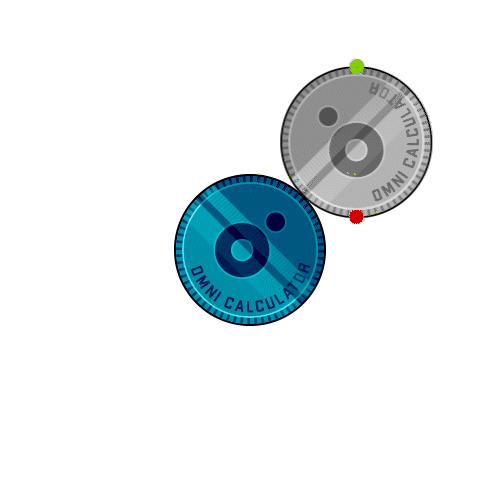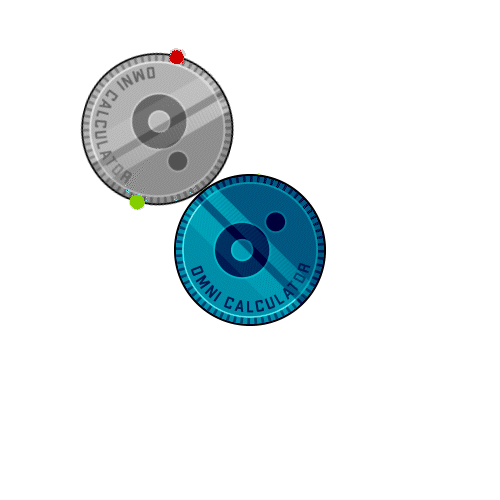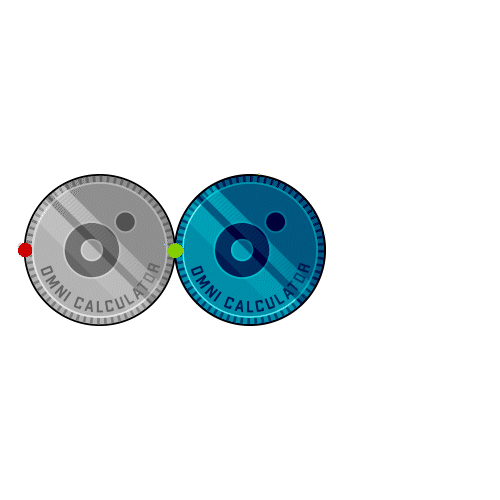
Definition: This calculator computes the number of rotations a smaller coin completes when it rolls around a larger fixed coin without slipping, based on the diameters of both coins.

Purpose: It helps users understand the coin rotation paradox, a counterintuitive phenomenon in geometry, with applications in education, engineering, and design.

2. How Does the Calculator Work?

The calculator uses the following method to compute the number of rotations:

Convert Diameters to Radii: $r_{f} = \frac{Diameter of Fixed Coin}{2}$ , $r_{r} = \frac{Diameter of Rotating Coin}{2}$
Number of Rotations: $N = 1 + \frac{r_{f}}{r_{r}}$ , where $r_{f}$ is the radius of the fixed coin and $r_{r}$ is the radius of the rotating coin.

Unit Conversions:

Input Dimensions: m, cm (1 m = 100 cm), mm (1 m = 1000 mm), in (1 m = 39.3701 in), ft (1 m = 3.28084 ft), yd (1 m = 1.09361 yd)

Steps:

Input the diameters of the fixed and rotating coins with their units.
Convert the diameters to radii in meters for calculation.
Validate the inputs (diameters must be positive).
Calculate the number of rotations using the formula.
Display the result, formatted to 4 decimal places.

3. Importance of Coin Rotation Paradox Calculations

Understanding the coin rotation paradox is crucial for:

Geometry Education: Illustrating the difference between rotation and revolution in circular motion.
Engineering Design: Designing gears, wheels, and rotating components where rotational dynamics are key.
Astronomy: Understanding concepts like sidereal time, where the Earth's rotation and revolution lead to similar paradoxical results.

4. Using the Calculator

Examples:

Example 1: For a fixed coin diameter of 24 mm and a rotating coin diameter of 24 mm (identical coins):
- Convert: Fixed coin radius $r_{f} = \frac{24}{2} = 12 mm = 0.012 m$ , Rotating coin radius $r_{r} = \frac{24}{2} = 12 mm = 0.012 m$
- Number of Rotations: $N = 1 + \frac{0.012}{0.012} = 1 + 1 = 2$
- Result: The rotating coin completes 2 rotations.
Example 2: For a fixed coin diameter of 30 mm and a rotating coin diameter of 10 mm:
- Convert: Fixed coin radius $r_{f} = \frac{30}{2} = 15 mm = 0.015 m$ , Rotating coin radius $r_{r} = \frac{10}{2} = 5 mm = 0.005 m$
- Number of Rotations: $N = 1 + \frac{0.015}{0.005} = 1 + 3 = 4$
- Result: The rotating coin completes 4 rotations.

5. Frequently Asked Questions (FAQ)

Q: What is the Coin Rotation Paradox?
A: The coin rotation paradox is a counterintuitive phenomenon where a coin rolling around another coin without slipping completes more rotations than expected. For identical coins, the rotating coin completes 2 rotations instead of the intuitive 1.

Q: Why does the rotating coin make more rotations than expected?
A: The extra rotation comes from the revolution around the fixed coin. The center of the rotating coin travels a path with a radius equal to the sum of the two radii, leading to an additional rotation beyond the rolling motion.