Circumcenter of a Triangle Calculator

\( x_1 \):

\( y_1 \):

\( x_2 \):

\( y_2 \):

\( x_3 \):

\( y_3 \):

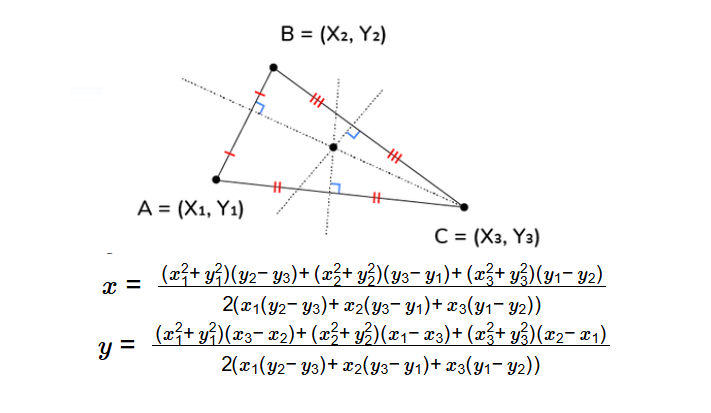
1. What is a Circumcenter of a Triangle Calculator?

Definition: This calculator determines the circumcenter of a triangle given the coordinates of its three vertices \( (x_1, y_1) \), \( (x_2, y_2) \), and \( (x_3, y_3) \). The circumcenter is the point where the perpendicular bisectors of the triangle's sides intersect, and it is equidistant from all three vertices. Coordinates are entered with a unit, and outputs can be converted independently, defaulting to meters (m).

Purpose: It aids in geometry education and practical applications by finding the circumcenter, useful in fields like engineering, computer graphics, and architecture for determining the center of the circumscribed circle.

2. How Does the Calculator Work?

The calculator uses the following formulas to find the circumcenter \( (x, y) \):

\( x = \frac{(x_1^2 + y_1^2)(y_2 - y_3) + (x_2^2 + y_2^2)(y_3 - y_1) + (x_3^2 + y_3^2)(y_1 - y_2)}{2(x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2))} \)
\( y = \frac{(x_1^2 + y_1^2)(x_3 - x_2) + (x_2^2 + y_2^2)(x_1 - x_3) + (x_3^2 + y_3^2)(x_2 - x_1)}{2(x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2))} \)

Steps:

Input the coordinates of the three vertices with their units (default: m).
Validate inputs: ensure the points are not collinear by checking the triangle's area.
Convert all coordinates to meters for calculation.
Compute the circumcenter coordinates using the formulas above.
Convert the output coordinates to the user-selected units (default: m).
Display the results to 4 decimal places.

3. Importance of Circumcenter of a Triangle Calculations

Circumcenter calculations are essential for:

Geometry: Determining the center of the circumscribed circle, which passes through all three vertices of the triangle.
Architecture: Designing structures that require circular arcs passing through specific points, often needing unit conversions (e.g., m to cm).
Computer Graphics: Positioning circular elements in 2D graphics or simulations with measurements in various units.

4. Using the Calculator

Examples:

Example 1: Vertices \( (0, 0) \) m, \( (3, 0) \) m, \( (0, 4) \) m, Circumcenter in m
Circumcenter: \( (x, y) = (1.5, 2) \) m = (150.0000, 200.0000) cm.
Example 2: Vertices \( (1, 1) \) cm, \( (5, 1) \) cm, \( (3, 4) \) cm, Circumcenter in cm
Convert to meters: \( (0.01, 0.01) \), \( (0.05, 0.01) \), \( (0.03, 0.04) \),
Circumcenter: \( (x, y) = (0.03, 0.02) \) m = (3.0000, 2.0000) cm.
Example 3: Vertices \( (-2, 3) \) ft, \( (4, 3) \) ft, \( (1, 7) \) ft, Circumcenter in ft
Convert to meters: \( (-0.6096, 0.9144) \), \( (1.2192, 0.9144) \), \( (0.3048, 2.1336) \),
Circumcenter: \( (x, y) = (0.3048, 1.2192) \) m = (1.0000, 4.0000) ft.

5. Frequently Asked Questions (FAQ)

Q: What is the circumcenter of a triangle?
A: The circumcenter is the point where the perpendicular bisectors of a triangle's sides intersect. It is equidistant from all three vertices and is the center of the circumscribed circle.

Q: Why do outputs default to meters?
A: Meters (m) are the default unit to provide a standard metric base, ensuring consistency in calculations, but you can convert each output to other units independently.

Q: Why must the points not be collinear?
A: If the points are collinear (lie on a straight line), they do not form a triangle, and the circumcenter is undefined. The calculator uses the Shoelace formula to check for collinearity.