Circle Theorems Calculator

Theorem:

Inscribed Angle \( \theta_i \) (degrees):

Radius:

Central Angle \( \theta_c \) (degrees):

Arc Length:

1. What is a Circle Theorems Calculator?

Definition: This calculator applies various circle theorems to compute geometric properties such as angles, arc lengths, chord lengths, and segment lengths.

Purpose: It assists in solving problems involving circle theorems, useful in geometry education, engineering, and design.

2. How Does the Calculator Work?

The calculator operates in five modes:

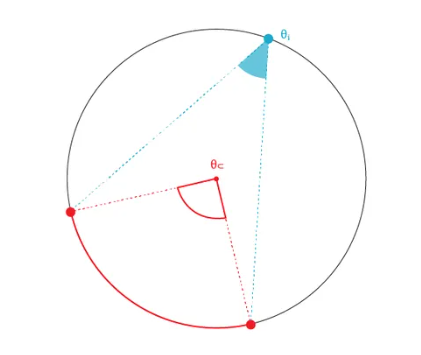
Inscribed Angle Theorem:

Central Angle \( \theta_c \): \( \theta_c = 2 \times \theta_i \)
Arc Length: \( \text{Arc Length} = r \times \theta_c \), where \( \theta_c \) is in radians

Thales Theorem (Angle in a Semicircle):

Diameter: \( \text{Diameter} = \sqrt{AB^2 + BC^2} \)
Angle \( \angle BAC \): \( \angle BAC = \arcsin\left(\frac{BC}{\text{Diameter}}\right) \)
Angle \( \angle ACB \): \( \angle ACB = \arcsin\left(\frac{AB}{\text{Diameter}}\right) \)

Cyclic Quadrilateral Theorem:

Angle C: \( \text{Angle C} = 180^\circ - \text{Angle A} \)
Angle D: \( \text{Angle D} = 180^\circ - \text{Angle B} \)

Chord Length Theorem:

Chord Length: \( \text{Chord Length} = 2 \times \sqrt{r^2 - d^2} \), where \( d \) is the distance from the center

Intersecting Secants Theorem:

Closest Angle \( \theta_1 \): \( \theta_3 = \frac{\theta_2 - \theta_1}{2} \)
PD Length: \( \text{PD} = \frac{\text{PB} \times \text{PC}}{\text{PA}} \)

Unit Conversions:

Input Dimensions: m, cm (1 m = 100 cm), mm (1 m = 1000 mm), in (1 m = 39.3701 in), ft (1 m = 3.28084 ft), yd (1 m = 1.09361 yd)
Output Dimensions: m, cm, mm, in, ft, yd

Steps:

Select the theorem (Inscribed Angle, Thales, Cyclic Quadrilateral, Chord Length, or Intersecting Secants).
View the corresponding diagram for the selected theorem.
Input the required values with their units.
Convert all dimensions to meters for calculation.
Validate the inputs (e.g., angle constraints, positive lengths).
Calculate the outputs based on the theorem's formulas, formatted to 4 decimal places or in scientific notation for very small values.

3. Importance of Circle Theorems Calculations

Calculating properties using circle theorems is crucial for:

Geometry Education: Understanding relationships between angles, chords, and arcs in circles.
Engineering Design: Designing circular components like arches or wheels.
Construction: Measuring material needs for circular structures.

4. Frequently Asked Questions (FAQ)

Q: What are circle theorems?
A: Circle theorems are geometric principles that describe relationships between angles, chords, arcs, and segments in a circle, such as the inscribed angle theorem, Thales theorem, and cyclic quadrilateral theorem.

J: Why are circle theorems important?
A: They are essential for solving geometric problems involving circles, with applications in education, engineering, and design.