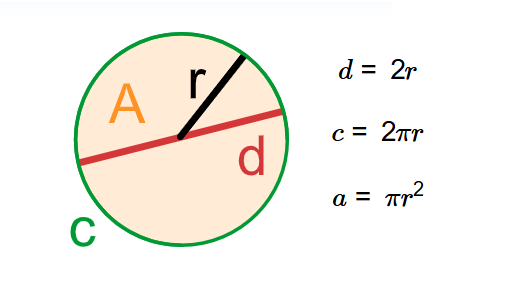Circle Formula Calculator

1. What is a Circle Formula Calculator?

Definition: This calculator computes the radius, diameter, circumference, and area of a circle based on one known value. The user selects the input parameter (radius, diameter, circumference, or area) and provides its value along with a unit, and the calculator computes the remaining parameters, allowing independent unit conversions for each output. Lengths default to meters (m), and areas default to square meters (m²).

Purpose: It aids in geometry education and practical applications by calculating circle properties, useful in fields like engineering, design, and physics for circular shapes.

2. How Does the Calculator Work?

The calculator uses the following formulas, where \( r \) is the radius, \( d \) the diameter, \( c \) the circumference, and \( a \) the area:

Diameter: \( d = 2r \)
Circumference: \( c = 2\pi r \)
Area: \( a = \pi r^2 \)

Steps:

Select the input parameter and its unit (default: m for lengths, m² for area).
Input the value.
Validate input: ensure the value is positive.
Convert the input to meters (or m² for area) and compute all parameters in meters.
Convert each output to the user-selected unit (default: m for lengths, m² for area).
Display the results to 4 decimal places.

3. Importance of Circle Formula Calculations

Circle formula calculations are essential for:

Geometry: Understanding the properties of circles and their parameters.
Engineering: Designing circular components like wheels or pipes, often requiring unit conversions (e.g., m to cm).
Physics: Analyzing circular motion or orbits with measurements in various units.

4. Using the Calculator

Examples:

Given Radius: Radius = 3 m,
Diameter: \( 2 \times 3 = 6.0000 \) m,
Circumference: \( 2 \times \pi \times 3 \approx 18.8496 \) m,
Area: \( \pi \times 3^2 \approx 28.2743 \) m²,
Converted: Diameter = 600.0000 cm, Area = 282743.3390 cm².
Given Diameter: Diameter = 10 cm,
Radius: \( 10 / 2 = 5.0000 \) cm = 0.0500 m,
Circumference: \( \pi \times 10 \approx 31.4159 \) cm = 0.3142 m,
Area: \( \pi \times (0.05)^2 \approx 0.0079 \) m² = 78.5398 cm².
Given Circumference: Circumference = 12.5664 m,
Radius: \( 12.566 cena4 / (2 \times \pi) \approx 2.0000 \) m = 200.0000 cm,
Diameter: \( 12.5664 / \pi \approx 4.0000 \) m,
Area: \( \pi \times (2)^2 \approx 12.5664 \) m² = 125663.7061 cm².
Given Area: Area = 50.2655 m²,
Radius: \( \sqrt{50.2655 / \pi} \approx 4.0000 \) m = 13.1234 ft,
Diameter: \( 2 \times 4 = 8.0000 \) m,
Circumference: \( 2 \times \pi \times 4 \approx 25.1330 \) m = 27.4943 yd.

5. Frequently Asked Questions (FAQ)

Q: What is the value of \( \pi \) used in the calculator?
A: The calculator uses \( \pi \approx 3.1415926535898 \), a high-precision approximation for accurate calculations.

Q: Why do outputs default to meters and square meters?
A: Meters (m) and square meters (m²) are the default units to provide a standard metric base, ensuring consistency in calculations, but you can convert each output to other units independently.

Q: Why must the input value be positive?
A: The radius, diameter, circumference, and area of a circle are geometric quantities that must be positive. A non-positive value would not represent a valid circle.