Circle Center Calculator

1. What is a Circle Center Calculator?

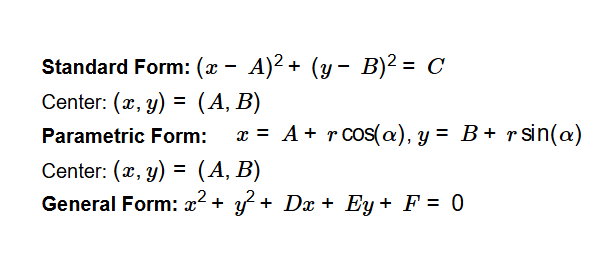
Definition: This calculator determines the center of a circle using three methods: Standard Form (\( (x - A)^2 + (y - B)^2 = C \)), Parametric Form (center derived from \( x = A + r \cos(\alpha) \), \( y = B + r \sin(\alpha) \)), and General Form (\( x^2 + y^2 + Dx + Ey + F = 0 \)). All inputs and outputs are treated as unitless numbers.

Purpose: It aids in geometry education and practical applications by finding the center of a circle, useful in fields like engineering, computer graphics, and design where circle equations are common.

2. How Does the Calculator Work?

The calculator uses the following methods:

Standard Form: \( (x - A)^2 + (y - B)^2 = C \)

Center: \( (x, y) = (A, B) \)

Parametric Form: Center derived from \( x = A + r \cos(\alpha) \), \( y = B + r \sin(\alpha) \)

Center: \( (x, y) = (A, B) \)

General Form: \( x^2 + y^2 + Dx + Ey + F = 0 \)

Center: \( (x, y) = \left(-\frac{D}{2}, -\frac{E}{2}\right) \)

Steps:

Select the calculation method.
Input the required values as unitless numbers.
Validate inputs: ensure \( C > 0 \) (Standard), \( r > 0 \) (Parametric), and the discriminant condition for General Form.
Compute the center coordinates using the appropriate method.
Display the results to 4 decimal places.

3. Importance of Circle Center Calculations

Circle center calculations are essential for:

Geometry: Understanding the properties of circles in different equation forms.
Engineering: Designing circular components like gears or wheels.
Computer Graphics: Positioning circles in 2D graphics or animations using parametric or standard forms.

4. Using the Calculator

Examples:

Standard Form: \( A = 2 \), \( B = 3 \), \( C = 25 \), Center
Center: \( (x, y) = (2, 3) \) = (2.0000, 3.0000).
Parametric Form: \( A = 1 \), \( B = -2 \), \( r = 5 \), Center
Center: \( (x, y) = (1, -2) \) = (1.0000, -2.0000).
General Form: \( D = -4 \), \( E = 6 \), \( F = -12 \), Center
Center: \( (x, y) = \left(-\frac{-4}{2}, -\frac{6}{2}\right) = (2, -3) \) = (2.0000, -3.0000).

5. Frequently Asked Questions (FAQ)

Q: What is the center of a circle?
A: The center of a circle is the point equidistant from all points on the circle's circumference. It is represented as \( (x, y) \) in the circle's equation.

Q: Why is the angle \( \alpha \) not required in the Parametric Form?
A: The angle \( \alpha \) determines a point on the circle, but the center is simply \( (A, B) \), which does not depend on \( \alpha \).

Q: What does the discriminant condition mean in the General Form?
A: In the General Form \( x^2 + y^2 + Dx + Ey + F = 0 \), the discriminant \( D^2 + E^2 - 4F \) must be positive for the equation to represent a circle. If it’s zero or negative, the equation may represent a point, a line, or no real shape.